|
MODELACIÓN
DISTRIBUIDA DE LA ESCORRENTÍA SUPERFICIAL EN PEQUEÑAS CUENCAS
MEDIANTE SIG. EVALUACIÓN EXPERIMENTAL
|
Martínez
Álvarez, V. ; Dal-Ré Tenreiro, R. ; García García,
A. I. ; Ayuga Téllez, F.
| RESUMEN Se ha desarrollado y evaluado experimentalmente un modelo hidrológico distribuido para la simulación de eventos en pequeñas cuencas no aforadas. El modelo, que ha sido implementado en el módulo matricial del sistema de información geográfica Arc/lnfo, aplica el método del número de curva del USDA SCS para sintetizar la lluvia neta en cada celda de la cuenca, que posteriormente es conducida hasta el punto de desagüe siguiendo los caminos de máxima pendiente. Es este proceso de traslación de la escorrentía se han estudiado varias superficies de fricción. Finalmente se obtiene el hidrograma del evento mediante el método de las isocronas. Los primeros resultados muestran una gran capacidad en la simulación de la forma del hidrograma, encontrándose el proceso crítico en la evaluación de la lluvia neta a partir de la precipitación total. Tras comparar los resultados con los obtenidos mediante la aplicación de varios modelos agregados clásicos para cuencas no aforadas, el tratamiento distribuido ha generado volúmenes de escorrentía y formas de los hidrogramas notablemente más próximos a los registrados en varias cuencas experimentales. | |
| SURFACE RUNOFF DISTRIBUTED MODELLING IN SMALL WATERSHEDS WITH GIS. EXPERIMENTAL EVALUATION ABSTRACT A Geographic Information System based distributed model that generates spatially surface runoff from precipitation and basin physical properties has been developed and tested in several small watersheds near Madrid. The model, implemented directly within the GRID module of Arc / Info GIS, generates effective rainfall using the USDA SCS curve number method. This cell-generated runoff is driven through the watershed from its location to the basin outlet. In this movement, several friction surfaces have been considered. Eventually, a time-area method is applied to obtain surface runoff hydrographs. Results indicate that proposed distributed models have considerable capacity in the simulation of hydrograph shape. However, the transition from total to effective rainfall offers an important limitation. Modelling results have been compared with the application of severallumped models for ungaged watersheds and distributed treatment has generated total runoff volumes and hydrograph shapes closer to real figures than lumped one. |
Palabras clave:
Hidrología; Modelo distribuido; SIG; Escorrentía superficial; Pequeñas cuencas;
Superficies de fricción.
1.
INTRODUCCIÓN
El notable incremento producido durante los últimos años en el
número de proyectos de pequeños embalses localizados en el medio
rural, que aprovechan las aguas de escorrentía de pequeñas cuencas
para abastecimiento de poblaciones y zonas de riego reducidas, hace recomendable
nuevos estudios sobre la determinación de sus parámetros hidrológicos
de diseño. Actualmente, entendemos por pequeñas cuencas aquellas
que, por ser de superficie inferior a los 50 km2, no han sido catalogadas individualmente
por la administración. Por este motivo su principal característica
es que carecen de datos de aforo y, por tanto, no es posible utilizar técnicas
hidrológicas de cuencas mayores, basadas en modelos que requieren la
existencia de dichos aforos para la calibración de sus parámetros.
Ante esta situación, el estudio de eventos hidrológicos y avenidas en las pequeñas cuencas se basa en el empleo de modelos que, partiendo de información meteorológica y de propiedades físicas y geomorfológicas fácilmente observables de la cuenca, nos permiten estimar el valor de los parámetros de diseño necesarios en numerosos proyectos de ingeniería. Los modelos habitualmente empleados en dichos estudios se clasifican como agregados, puesto que consideran que la lluvia es uniforme sobre la cuenca y que los parámetros del modelo son globales y constantes durante cada evento. Sin embargo, las últimas tendencias de los estudios hidrológicos en cuencas mayores se basan en la modelación distribuida de los procesos implicados, lo que supone considerar la variabilidad espacial de la información sobre la cuenca anteriormente mencionada. Esta consideración supone un mayor acercamiento a la realidad de los procesos hidrológicos, puesto que es evidente que existe una variabilidad espacial natural de la precipitación, de los parámetros implicados en la infiltración y de la estructura de la red de drenaje. Consecuentemente, existen importantes ventajas teóricas de los modelos distribuidos respecto a los modelos agregados empleados habitualmente, al igual que un notable incremento de complejidad en su aplicación, asociado al considerable aumento en el volumen de información requerido. Esta circunstancia, junto a una serie de cuestiones relacionadas con la modelación distribuida como son los efectos de escala y la naturaleza de los modelos a emplear, ha originado un interesante debate científico sobre su aplicabilidad (Abbott et al., 1986; Wood et al, 1988 y Beven 1991).
La importante capacidad actual de los Sistemas de Información Geográfica (SIG) para manejar y analizar información espacial, hace de estas herramientas informáticas un entorno adecuado para afrontar de manera eficiente la modelación hidrológica distribuida. De esta manera, Maidment (1993) emplea los SIG para definir el concepto del hidrograma unitario distribuido, que supone una nueva perspectiva para afrontar la aplicación de los SIG a la modelación de eventos hidrológicos. Frutos de este nuevo concepto son la reciente publicación de trabajos sobre la modelación distribuida con SIG como los de Muzik (1996) y Tung (1998), que se centran en cuencas de tamaño medio y carecen de comprobación experimental. En España destacan los modelos distribuidos con pocos parámetros propuestos por Francés y Benito (1995) y contrastados experimentalmente en la cuenca del río Palancia, también de tamaño superior a las que centran nuestro interés.
Ante esta perspectiva, se ha considerado oportuno contrastar las posibilidades de la modelación hidrológica distribuida para la simulación de eventos hidrológicos en pequeñas cuencas rurales no aforadas. Para ello, se han adaptado las técnicas que vienen siendo utilizadas habitualmente en la resolución de este tipo de problemas (Dal-Ré y Ayuga, 1996) a las posibilidades analíticas que nos ofrecen los SIG. El resultado ha sido un modelo implementado íntegramente en el modulo matricial del SIG ArcInfo (Martínez, 1999), así como su evaluación experimental en dos pequeñas cuencas piloto. El modelo plantea distintas soluciones para cada etapa del proceso, como son el tratamiento de la precipitación, la generación de escorrentía, el desplazamiento de la misma sobre la cuenca y la obtención de hidrogramas. Se ha prestado especial atención al proceso de traslación de la escorrentía, proponiéndose varias superficies de fricción de distinta complejidad.
Los hidrogramas
simulados se han comparado con los registrados en dos cuencas piloto y con los
obtenidos tras la aplicación de dos modelos agregados, basados en el
concepto del hidrograma unitario, de uso habitual en nuestro país:
El método del hidrograma unitario adimensional del USDA SCS, aplicado
mediante el empleo del programa HEC-1 (U. S. Army Corps of Engineers, 1985).
El método del hidrograma unitario triangular de Témez (MOPU,
1987). Para su aplicación se ha utilizado la hoja de cálculo Microsoft
Excel.
2.
CUENCAS EXPERIMENTALES Y EQUIPOS INSTALADOS
Para el contraste de los modelos propuestos se dispone, desde principios de
1998, de los datos obtenidos en dos pequeñas cuencas experimentales en
la Comunidad de Madrid, de relieves suaves y sin actividades humanas que alteren
su funcionamiento hidrológico natural. La primera es la cuenca de arroyo
del Monte, que se localiza en el término municipal de Daganzo de Arriba,
y tiene una extensión aproximada de 7 km2. Sus suelos son de textura
franco arcillo arenosa y predomina claramente el cultivo de cereal en año
y vez. La segunda en la cuenca del arroyo de Valdelamasa, localizada en los
términos municipales de Madrid y Colmenar Viejo y que tiene una extensión
de 17 km2. Sus suelos son de textura franca y franco arenosa, con un uso mixto
entre encinar adehesado y cereal en año y vez. La FIGURA 1 muestra los
Modelos Digitales del Terreno (MDT) de ambas cuencas.
FIGURA 1. Modelos Digitales del Terreno de las cuencas experimentales
En cada una de las cuencas se ha realizado una obra de aforo, consistente en
la transformación del cauce natural en un canal de sección trapecial
en hormigón armado de 4 m de longitud. En el fondo de dicho canal se
han instalado dos sensores. El primero es una membrana de presión que
mide la altura de agua sobre el canal. El segundo un emisor-receptor de ondas
de alta frecuencia, que relaciona el efecto Doppler producido en las ondas reflejadas
por las partículas en suspensión con la velocidad del flujo en
la sección. Conociendo el área de la sección mojada y la
velocidad en la misma se obtiene el caudal en cada instante. Estos sensores,
al igual que un pluviómetro de cazoletas de 0.1 mm de sensibilidad, están
conectados a un data-logger que almacena las lecturas a intervalos de 15 minutos.
Estos datos se recogen mensualmente por medio de un ordenador portátil.
3.
COMPONENTES DEL MODELO
Cualquier modelo distribuido orientado a la simulación de eventos hidrológicos
en pequeñas cuencas debe tratar tres problemas básicos:
3.1. Tratamiento de la precipitación
La información pluviométrica actualmente disponible en pequeñas
cuencas puede dar lugar a dos situaciones concretas: existencia de datos de precipitación
dentro de la cuenca o ausencia de los mismos. Si somos conscientes de que la densidad
media de estaciones pluviométricas en nuestro país es aproximadamente
de una cada 250 km2, nos daremos cuenta que al estudiar una pequeña cuenca
lo más probable es que nos encontremos en el segundo caso. A pesar de ello,
la heterogeneidad en la distribución de las estaciones proporciona una
casuística muy variada que el modelo debe ser capaz de considerar. Por
este motivo, el modelo esta preparado tanto para el tratamiento distribuido de
la precipitación mediante métodos como los polígonos de Thiessen
y el inverso de las distancias al cuadrado, que asignan en cada celda una magnitud
de precipitación bruta para cada intervalo en función de los datos
recogidos en una serie de puntos de la cuenca, como para su tratamiento agregado
a partir de un único punto de información, que asigna las mismas
magnitudes de precipitación para todas las celdas de la cuenca. En todos
los casos el resultado es una serie de coberturas de precipitación en función
del intervalo de tiempo seleccionado.
3.2.
Síntesis de la lluvia efectiva en cada celda de la cuenca
Una vez asignado un valor de precipitación a cada celda para cada intervalo
de tiempo considerado, el modelo debe evaluar la lluvia neta, es decir, la porción
de la precipitación total que se convierte en escorrentía. Para
ello se ha utilizado el método del número de curva (USDA SCS,
1985) ya que, además de su simplicidad y claridad conceptual, ofrece
las siguientes ventajas:
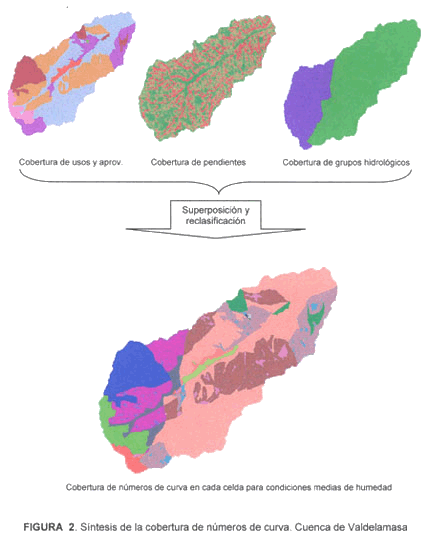
FIGURA 2. Síntesis de la cobertura de números de curva. Cuenca de Valdelamasa
Conocida la cobertura de números de curva, se aplica el método
para cada intervalo de tiempo considerado, determinándose la escorrentía
acumulada que se produce en cada celda hasta dicho intervalo, en función
únicamente de la precipitación total acumulada hasta ese instante
y de la cobertura de información de números de curva. Posteriormente,
por diferencia entre coberturas sucesivas de escorrentía acumulada
se calcula la serie de coberturas de lluvia neta en cada intervalo.
3.3.
Traslación de la lluvia efectiva generada en cada celda hasta la salida
de la cuenca
La lluvia efectiva que se genera en cada punto de la cuenca comienza su movimiento
a favor de la máxima pendiente dando lugar a la escorrentía
superficial, cuyo resultado final será un hidrograma en la salida de
la cuenca. Dentro de los modelos conceptuales de traslación, la técnica
más experimentada es la del hidrograma unitario. Esta técnica
se basa en la hipótesis de que el sistema lluvia neta-escorrentía
sea un sistema lineal invariante en el tiempo, y en las consecuencias que
de la misma se derivan. Esta hipótesis, a pesar de las simplificaciones
que para el cálculo supone, puede implicar errores considerables ya
que la velocidad de desplazamiento del flujo, ya sea en ladera o encauzado,
depende de la magnitud de los caudales circulantes y, por tanto, de la intensidad
de la lluvia neta.
Con el fin de
abordar esta problemática, se han estudiado tres soluciones para resolver
la traslación de la escorrentía, todas ellas basadas en el cálculo
de una cobertura de tiempos de paso de la escorrentía por cada celda
de la cuenca, en el cálculo de la correspondiente cobertura de tiempos
de viaje desde cada una de las celdas hasta el punto de desagüe y en
la aplicación del concepto del hidrograma unitario distribuido rectangular
(Maidment, 1993), para posteriormente sintetizar el hidrograma del evento
mediante la aplicación del método de las isocronas. Cada una
de las soluciones planteadas se caracteriza por la metodología seguida
para obtener la cobertura de tiempo por unidad lineal que tarda el flujo en
recorrer cada una de las celdas, denominada habitualmente cobertura de tiempos
de paso o superficie de fricción. Las etapas seguidas en esta fase
de la modelación distribuida son las siguientes:
Cálculo de la cobertura de direcciones de flujo: a partir del
análisis geomorfológico de la zona de estudio, el SIG nos proporciona
una cobertura con la dirección del flujo en cada celda suponiendo que
se produce en la dirección de la máxima pendiente, así
como la delimitación de la cuenca vertiente al punto de estudio (FIGURA
3).
FIGURA 3. Cobertura de direcciones de flujo a partir del MDT. Cuenca de Valdelamasa
Calculo de las coberturas de superficie drenante a cada celda de la cuenca y de longitud de escorrentía desde las divisorias de agua a partir de análisis de la cobertura de direcciones de flujo. Estas coberturas se emplearán posteriormente para definir el tipo de flujo que se produce en cada celda.
Cálculo
de las superficies de fricción o coberturas de tiempos de paso de la
escorrentía por cada celda. Las tres propuestas estudiadas en esta
etapa del modelo son las siguientes:
Superficie
de fricción Nº1, velocidad constante en función del tiempo
de concentración (Tc). Esta propuesta asigna una velocidad del flujo
constante para toda la cuenca en función del tiempo de concentración
de la misma, que es calculado por medio de la expresión propuesta por
Kirpich:
![]() (1)
(1)
donde L representa la longitud del cauce principal de la cuenca hasta
la divisoria de aguas en km e I representa la pendiente media del cauce
principal, que son obtenidos a partir del análisis geomorfológico
del MDT. Conocido el Tc, se divide el mismo por la longitud del trayecto recorrido
siguiendo el camino de máxima pendiente desde el punto hidráulicamente
más alejado hasta el punto de desagüe de la cuenca, de modo que
se obtiene un tiempo de paso por unidad lineal que se aplicará a toda
la cuenca estudiada.
Superficie de fricción Nº2, Velocidad variable según
las expresiones del USDA SCS. El USDA SCS (1986) propone un método
alternativo para el cálculo del Tc, que consiste en la diferenciación
de los tipos de flujo por los que pasa la escorrentía generada en el
punto hidráulicamente más alejado del punto de desagüe
de la cuenca, para finalmente obtener el Tc como suma del tiempo consumido
en cada uno de los tramos diferenciados. Para ello distingue tres tipos de
flujo: flujo en ladera, flujo encauzado y flujo mixto. Las expresiones propuestas
nos permiten asignar tiempos de paso variables en cada una de las celdas de
la cuenca en función de las características geomorfológicas
de la misma.
El SCS propone calcular el tiempo de viaje del flujo en ladera mediante
una aproximación a la solución del flujo en ladera atribuida
a Overton y Meadows (1976):
![]() (2)
(2)
donde nl representa el coeficiente de rugosidad de Manning para flujo en ladera
tabulado en función del tipo de cubierta vegetal (Engman, 1986), L
representa la longitud de escorrentía en metros, P2 representa la máxima
precipitación en mm durante 24 horas para un periodo de retorno
de 2 años e I representa la pendiente del tramo. Si aplicamos
la misma expresión para una longitud de escorrentía inferior
en la anchura de celda a la real y la descontamos del valor anteriormente
calculado obtendremos el tiempo que tarda en ser recorrida cada celda. Este
tiempo dividido entre la anchura de la celda nos proporcionará el tiempo
de paso por unidad lineal para el caso de flujo en ladera.
Para las celdas con flujo encauzado, se calcula el tiempo de paso aplicando
la ecuación de Manning para flujo en canal, considerando una longitud
de un metro y la magnitud de los flujos circulantes correspondiente a un periodo
de retorno de 2 años:
![]() (3)
(3)
donde n representa el coeficiente de rugosidad de Manning para flujo encauzado
tabulado en función de las características del cauce y Rh representa
el radio hidráulico del cauce principal en metros.
Se ha considerado que en los primeros 100 m de longitud de escorrentía
se produce flujo en ladera y en las celdas con más de 1 km2 de superficie
drenante se produce flujo encauzado, mientras que en las celdas que no cumplen
ninguna de las condiciones anteriores se produce flujo mixto. Siguiendo los
criterios del USDA SCS, para asignar un tiempo de tránsito al flujo
mixto se adopta nuevamente la ecuación de Manning para flujo en canal,
pero se aplican unos valores constantes para el radio hidráulico Rh
y para el coeficiente de rugosidad n de 0.122 m y 0.05 respectivamente.
FIGURA 4. Superficie de fricción según criterios del USDA SCS. Cuenca de Valdelamasa
Superficie de
fricción Nº3. Velocidad variable considerando la intensidad de
la lluvia efectiva. De forma similar al caso anterior, el método propuesto
diferencia entre flujo en ladera y flujo encauzado. Para ello utiliza expresiones
que asignan una velocidad a cada celda en función de sus características
de pendiente y rugosidad, así como de la intensidad de lluvia efectiva
característica del evento estudiado, por lo que se superan las limitaciones
conceptuales del hidrograma unitario. Para el tratamiento del flujo en ladera
se propone una solución basada en la teoría de al onda cinemática,
aplicada a planos inclinados y considerando flujo turbulento:
![]() (4)
(4)
donde i representa
la intensidad de lluvia efectiva característica del evento. El resto
de variables y el procedimiento seguido para obtener los tiempos de paso para
flujo en ladera coinciden con los del caso anterior.
Para el cálculo
del tiempo de viaje en condiciones de flujo encauzado se propone aplicar la
ecuación de Manning para flujo en canal, pero considerando la magnitud
de los flujos circulantes correspondiente al evento estudiado, que se obtienen
a partir de la intensidad media de la lluvia neta durante el evento en la
superficie tributante a cada celda.
Cálculo
de la cobertura de tiempos de viaje desde cada celda al punto de desagüe
como suma de los tiempos de paso consumidos en recorrer el camino de máxima
pendiente. La FIGURA 5 recoge las coberturas de tiempos de paso para cada
superficie de fricción estudiada.
Cálculo
de la cobertura de isocronas. Para obtener el mapa de isocronas basta con
reclasificar los tiempos de viaje de acuerdo a la discretización temporal
elegida (FIGURA 5).
FIGURA 5. Coberturas de tiempos de viaje e isocronas obtenidas
tras aplicar cada una de las superficies de fricción estudiadas. Cuenca
de Valdelamasa
Obtención de hidrogramas. A partir de la capa de isocronas y conociendo
la escorrentía generada en cada celda y en cada intervalo de tiempo,
podemos conocer el hidrograma del evento en la celda de estudio aplicando
la expresión:
![]() (5)
(5)
donde Qi es el caudal que pasa en el instante i por el punto de análisis y E(j,i-j) es la lluvia neta generada en la isoyeta j durante el intervalo (i-j).
4.
IMPLEMENTACIÓN DEL MODELO EN EL SIG ARC/INFO
La ejecución de los procedimientos descritos implica un largo proceso
de cálculo mediante instrucciones que deben ser suministradas al SIG,
por lo que su utilización reiterada sin una serie de rutinas que agrupen
estas instrucciones sería prácticamente inabordable. Para poder
programar rutinas de esta complejidad sobre SIG son necesarios lenguajes de
programación diseñados especialmente para estas tareas, así
como que el propio SIG tenga implementadas numerosas funciones de interés
hidrológico que permitan abordar la modelación distribuida.
En este sentido, se ha optado por utilizar el SIG Arc/Info, de la empresa
norteamericana Environmental Systems Research Institute (ESRI), que contiene
un potente lenguaje de programación (ARC Macro Language) y dispone
de las funciones hidrológicas más actuales desarrolladas en
estos entornos de trabajo.
El modelo programado está estructurado en una serie de tareas iterativas que conducen al usuario desde el tratamiento de la precipitación hasta la síntesis final del hidrograma, debiendo elegir en cada uno de los procesos entre las distintas opciones programadas, en función de los datos disponibles para cada cuenca. Se trata de una estructura secuencial, por lo que el usuario debe ejecutar las rutinas correspondientes a unos procesos antes de comenzar con las siguientes (FIGURA 6). También se ha desarrollado un interfaz de usuario sencillo, constituido por barras de menús y ventanas, con el fin de facilitar el uso del modelo a usuarios no familiarizados con los SIG.
5.
HIDROGRAMAS REGISTRADOS Y TRATAMIENTO DE LOS MISMOS
Como se mencionó anteriormente, para el contraste de los modelos estudiados
se dispone de los datos registrados en dos pequeñas cuencas experimentales.
Hasta el momento se han registrado 5 eventos significativos, tres en la cuenca
del arroyo del Monte y dos en la del arroyo de Valdelamasa (TABLA 1).
|
Localización
|
Fecha
|
Precipitación
|
Volumen
total
|
Caudal
máximo
|
|
Arroyo
del Monte
|
11-05-98
|
24.3
mm
|
4542
m3
|
789.23
l/s
|
|
Arroyo
del Monte
|
05-06-98
|
15.7
mm
|
3317
m3
|
423.57
l/s
|
|
Arroyo
del Monte
|
25-09-98
|
17.5
mm
|
2857
m3
|
458.31
l/s
|
|
Arroyo
de Valdemasa
|
24-05-98
|
23.9
mm
|
6613
m3
|
576.12
l/s
|
|
Arroyo
de Valdemasa
|
05-05-98
|
22.9
mm
|
7193
m3
|
459.91
l/s
|
TABLA 1. Información de los eventos registrados
Los hidrogramas registrados en las cuencas experimentales corresponden a escorrentías totales, mientras que los modelos programados estudian escorrentías directas, que es la porción de la escorrentía total distinta al flujo base. Por este motivo, en los hidrogramas registrados deben separarse los hidrogramas de flujo base y de escorrentía directa para poder comparar estos últimos con los obtenidos mediante la aplicación de los modelos. La separación de hidrogramas constituye más un arte que una ciencia. Existen varios métodos para realizar esta tarea, sin que se pueda afirmar nada sobre la calidad de cada uno de ellos por falta de experimentación. En este trabajo se ha seguido el método de separación mediante una línea recta entre el inicio del hidrograma de escorrentía directa y el final del mismo. Se ha elegido este método por ser el más habitualmente empleado por otros autores, probablemente debido a su sencillez. La clave en la aplicación de este método se encuentra en la determinación del momento en que termina el hidrograma de escorrentía directa, puesto que el momento de inicio se hace coincidir con el del hidrograma de escorrentía total. La determinación del punto donde finaliza la escorrentía directa se basa en el criterio de que la curva de recesión del flujo base se ajusta a una curva exponencial decreciente del tipo:
![]() (6)
(6)
donde a representa el coeficiente de recesión
de la curva. De esta manera, si se procede a representar gráficamente
los logaritmos de los caudales frente al tiempo, el instante en que estos
se alejan de la recta en que se transforma la exponencial decreciente será
el punto elegido como inicio de la curva de recesión, y por tanto también
el final de la escorrentía directa. Hay que señalar que la sensibilidad
a esta operación en la zona del inicio y pico del hidrograma es escasa,
pero no así en la forma de la rama descendente, en la que la posición
del final de la escorrentía directa pasa a ser un elemento clave en
la pendiente y duración de la misma. La escorrentía directa
obtenida será la utilizada para evaluar los modelos distribuidos programados.
6.
RESULTADOS
Por lo que se refiere al paso de precipitación total a lluvia neta,
en la TABLA 2 se recogen los volúmenes totales de escorrentía
directa producidos en los eventos registrados así como los volúmenes
obtenidos mediante la aplicación distribuida y agregada del método
del NC. Cabe destacar que todos los eventos se han producido en condiciones
de humedad antecedente secas (AMCI) y que también se muestran los resultados
para las tres condiciones de humedad posibles (AMCI, AMCII y AMCIII), así
como para una intermedia entre las condiciones de humedad secas y medias (resultado
de aplicar el NC medio entre las mismas y denominada AMCI-II).
|
Evento
|
Volumen
|
Aplicación
distribuida del método del número de curva (m3)
|
Aplicación
agregada del método del número de curva (m3)
|
||||||
|
AMCI
|
AMCI-II
|
AMCII
|
AMCIII
|
AMCI
|
AMCI-II
|
AMCII
|
AMCIII
|
||
|
Monte
11.05.98 |
3818
|
3444
|
18774
|
61725
|
116441
|
0
|
365
|
10148
|
49693
|
|
Monte
05.06.98 |
2300
|
0
|
1531
|
14718
|
62170
|
0
|
0
|
416
|
17099
|
|
Monte
25.09.98 |
1912
|
0
|
5194
|
24334
|
74825
|
0
|
0
|
1442
|
22943
|
|
Valdelamasa
24.05.98 |
3606
|
254
|
302
|
10487
|
82411
|
0
|
0
|
0
|
4931
|
|
Valdelamasa
05.06.98 |
3456
|
235
|
284
|
8593
|
77412
|
0
|
0
|
0
|
3282
|
TABLA 2. Volúmenes de escorrentía simulados y observados
Los resultados ponen de manifiesto una de las cuestiones ampliamente discutidas por diversos autores: la diferenciación entre únicamente tres niveles de humedad resulta claramente insuficiente, puesto que las escorrentías obtenidas para cada estado de humedad difieren enormemente entre si, siendo necesario el empleo de relaciones de mayor continuidad entre el NC y la precipitación antecedente o cualquier otro parámetro fácilmente estimable. Además, para precipitaciones de magnitud ordinaria, como son las correspondientes a los eventos estudiados, pequeños errores en la determinación del NC producen errores de gran cuantía en la estimación de los volúmenes de escorrentía directa. Cabría esperar una mejor respuesta del método con precipitaciones de mayor magnitud, próximas a condiciones de diseño, pero hasta el momento no se dispone de datos que corroboren esta circunstancia.
La aplicación
distribuida del método ofrece resultados considerablemente mejores
que la aplicación agregada del mismo como consecuencia de la capacidad
de considerar la variabilidad espacial del NC en la cuenca. Lógicamente,
este hecho se manifiesta más intensamente en la cuenca del arroyo de
Valdelamasa debido a su mayor heterogeneidad, lo que implica que en la aplicación
agregada del método haya que considerar hasta condiciones de humedad
antecedente húmedas (AMCIII) para obtener valores próximos a
los observados, mientras que en la aplicación distribuida con condiciones
de humedad antecedente medias ya se superan ampliamente los volúmenes
observados.
Para comprobar la calidad de los modelos de traslación del flujo se
han eliminado los posibles errores arrastrados del modelo de infiltración
ajustando el volumen total de escorrentía producida a la registrada
en los equipos. Para ello, se ha introducido un valor corrector ? único
para toda la cuenca en la ecuación del método del NC (Francés
y Benito, 1995):
![]() (7)
(7)
![]() (8)
(8)
de forma que el factor corrector m nos sirve para
cubrir los errores en magnitud de las tablas del NC, manteniendo las relaciones
de proporcionalidad entre ellos. Las FIGURAS 6 y 7 muestran los hidrogramas
distribuidos y agregados correspondientes a uno de los eventos registrados
tras eliminar los posibles arrastrados del modelo de infiltración.
FIGURA
6. Evaluación de los modelos distribuidos de translación
estudiados.
(Evento del 11-05-1998, cuenca del arroyo del Monte)
Los resultados muestran un excelente ajuste del tratamiento distribuido mediante la superficie de fricción Nº3 en la forma y punta del hidrograma, así como en los tiempos de inicio y punta, mejorando notablemente los resultados obtenidos aplicando las otras dos opciones planteadas. Los errores porcentuales en los caudales punta se mantienen por debajo del 5% en todos los casos, excepto en el evento del 24 de abril de 98 en la cuenca del arroyo de Valdelamasa, donde se incrementa hasta el 27%. La forma de la rama descendente del hidrograma también es simulada con notable exactitud, siendo esta circunstancia especialmente significativa ante la gran dificultad que presenta su correcta simulación, manifestada por numerosos autores.
Las superficies de fricción Nº1 y Nº2 ofrecen respuestas similares, a pesar de que existen diferencias significativas en la forma de sus hidrogramas unitarios. En ambos casos se producen caudales punta superiores entre un 30 y un 130% a los observados. Sus hidrogramas simulados se ajustan bien a los observados en el inicio de la rama ascendente, pero se prolonga durante más tiempo, lo que deriva en mayores caudales punta y en unas ramas descendentes del hidrograma mucho más pronunciadas.
Esta diferencia entre los resultados ofrecidos por las superficies de fricción estudiadas puede justificarse por el hecho de que estamos estudiando eventos de pequeña magnitud. De esta manera, tanto la propuesta de velocidad constante en función del Tc como la de velocidad variable según las recomendaciones del USDA SCS ofrecen velocidades de desplazamientos correspondientes a condiciones de diseño, es decir, a magnitudes e intensidades de precipitación bastante superiores y, por tanto, producen respuestas más rápidas de la cuenca. Sin embargo, la superficie e fricción Nº3 es capaz de reflejar la influencia de la intensidad característica de lluvia efectiva producida por el evento, produciendo una respuesta más amortiguada y próxima a la observada como consecuencia de asignar tiempos de paso mayores en cada celda. Es de esperar que conforme aumente la magnitud de la precipitación los resultados ofrecidos por los tres modelos estudiados se aproximen.
Las respuestas bruscas producidas por la propuesta de velocidad constante en función del Tc ya fueron indicadas por Francés y Benito (1995), en sus esfuerzos por modelar de forma distribuida las avenidas en la cuenca del río Palancia. En esta ocasión, Francés afrontó el problema mediante el artificio de suponer que la respuesta de la escorrentía generada en cada celda y en cada intervalo de tiempo se ajustaba a la de un embalse o almacenamiento lineal, mediante la utilización del hidrograma unitario de Clark, lo que producía un amortiguamiento de los hidrogramas simulados. En nuestro caso, la simple diferenciación entre flujo en ladera y flujo encauzado y el estudio de cada uno de ellos considerando la intensidad de la lluvia neta característica de cada evento, ha producido efectos similares a los obtenidos por Francés mediante el empleo del hidrograma unitario de Clark.
FIGURA
7. Evaluación de los modelos agregados de translación.
(Evento del 11-05-1998, cuenca del arroyo del Monte)
Los resultados de la aplicación de los modelos agregados muestran unos ajustes que en general pueden considerarse aceptables, como era de esperar de unos métodos ampliamente experimentados y de gran aceptación. Los ajustes son mejores que en el caso de los modelos distribuidos con las superficies de fricción Nº1 y Nº2, que adolecen del problema mencionado anteriormente. Sin embargo, son claramente inferiores a los ofrecidos por la Nº3. Los resultados ofrecidos por los dos modelos considerados no son homogéneos puesto que el método del hidrograma unitario adimensional del USDA SCS ofrece mejores resultados que el método del hidrograma unitario triangular de Témez en la cuenca del arroyo del Monte, mientras que en la cuenca del arroyo de Valdelamasa ocurre lo contrario.
7.
CONCLUSIONES
Los modelos hidrológicos distribuidos implementados sobre SIG nos ofrecen
una nueva perspectiva para afrontar el estudio hidrológico de eventos
en pequeñas cuencas a partir de sus propiedades físicas y geomorfológicas,
con importantes ventajas frente a los sistemas clásicos. Las principales
derivan de la posibilidad de considerar la variabilidad espacial de la información
implicada, lo que a posteriori implica un considerable incremento en la calidad
de los resultados frente al tratamiento clásico con modelos agregados.
A la vista del análisis de los datos registrados en dos pequeñas cuencas experimentales durante los últimos 2 años, se puede afirmar que el proceso crítico en la simulación de eventos es la evaluación de la lluvia neta a partir de la precipitación total. La metodología del NC plantea una problemática importante por el tratamiento que recibe el estado de humedad antecedente y no existen otras metodologías de fácil aplicación que supongan una alternativa clara. Ante esta situación, se hace necesario plantear posibles mejoras que proporcionen una relación continua entre el NC y el estado de humedad antecedente. Por lo que se refiere a las superficies de fricción empleadas para el estudio de la translación de la escorrentía, los datos registrados muestran que la superficie Nº3 incrementa notablemente la calidad de los resultados obtenidos mediante los modelos agregados más habituales. Sin embargo, la modelación distribuida utilizando las otras superficies de fricción estudiadas produce respuestas muy bruscas, que no mejoran los resultados de los modelos agregados.
Finalmente, hay que destacar la gran cantidad de información adicional que se genera durante la modelación distribuida, como los campos de magnitudes y velocidades del flujo sobre la cuenca, que puede ser de gran utilidad para su aplicación en estudios medioambientales relacionados con los procesos erosivos o contaminantes.
|
Abbott,
M. B.; Bathurst, J. C.; Cunge, J. A.; O’Connell, P. E. y Rasmussen,
J., 1986. An introdution to the European Hydrological System, SHE. History,and
philosophy pf a physically.based, distributed modelling system. Journal
of Hydrology, 87; 45-59. |
| SUMARIO |