SUMARIO

VIRGINIA RUIZ FERRER (*); ANTONIO RUIZ MATEO (**)

RESUMEN En los procesos de desinfección, se han venido proponiendo diversos modelos de leyes de decrecimiento de la población bacteriana para tener en cuenta las desviaciones sistemáticas que se obtienen experimentalmente respecto a la conocida ley exponencial-lineal. En el presente artículo se propone una explicación de estas desviaciones basada en lo que hemos denominado hipótesis de población infinitamente segregada, que consiste en suponer que en el instante inicial la población de microorganismos está compuesta por una distribución continua de subpoblaciones con distinta capacidad de supervivencia, pero manteniendo la hipótesis de que dentro de cada subpoblación, el decrecimiento sigue una ley exponencial-lineal de parámetro k, para un cierto intervalo de valores que suponemos comprendido entre k = ¥. A partir de esta hipótesis se demuestra que la ley de decrecimiento de la concentraciones es la transformada de Laplace de la función de reparto inicial, lo que permite obtener una amplia gama de leyes de decrecimiento. En particular, todas las leyes propuestas están asociadas a las respectivas funciones de reparto que se calculan en el artículo. Se propone una función de reparto inicial sobre la base de que sea autorreproducible, ya que no parece lógico que el tipo de función dependa del momento en que empecemos a hacer las medidas. Dicha función coincide con la distribución gamma de la Teoría de probabilidades, lo que nos ha permitido conocer rápidamente muchas de sus propiedades. Su transformada de Laplace nos da una ley de decrecimiento de tipo hiperbólico con dos parámetros que en general habrá que calcular por ajuste no lineal con los datos experimentales. No obstante, se dan algunas reglas y ejemplos que facilitarán dicho ajuste en la práctica. Finalmente se comentan otras hipótesis que también conducen a la ley hiperbólica de decrecimiento.

MICROORGANISM CONCENTRATION DECAY DURING WASTEWATER TREATMENT ABSTRACT In disinfection processes, different models of bacterial population decay have been proposed to acrount for the systematic deviations from the well-known linear-exponential model that experimental results show. In this article, an explanation for these deviations is proposed based in what here it is called hypothesis of infinitely segregated population. Under this hypothesis it is supossed that initially the microorganism population is composed of a continous distribution of subpopulations with different survival capacity, but retaining for each subpopulation a linear-exponential behaviour with parameter k, which ranges between k = 0 (no mortality) and k = ¥ (instant mortality). Based on this hypothesis it is proved that the law of concentration decay is the Laplace transform of the initial distribution function, what allows for a wide range of decay laws. As a matter of fact, the initial distribution function associated to every decay law proposed up to date is calculated in this paper. As it is likely that the type of initial distribution function does not depend on the time the experiment starts, a selfreproductive function is proposed. This function coincides with the gamma distribution of Probability Theory, which allows to deduce easily many interesting properties. Its Laplace transform happens to be a two-parameter hyperbolic decay law. The parameters are to be calculated fitting the law to experimental results by non-linear regression. However, some rules and examples are provided in order to make easier the fitting task. Finally, other hypothesis leading also to the hyperbolic decay law are commented.

Palabras clave: Desinfección de aguas residuales; Inactivación de bacterias fecales en aguas; Supervivencia de microorganismos; Resistencia microbiana a la desinfección.

INTRODUCCIÓN

En Ingeniería del Saneamiento son muchos los procesos orientados a la eliminación de microorganismos patógenos. Dejando aparte los fenómenos de sedimentación y filtración, los demás se basan en crear unas condiciones adversas para la supervivencia de estos organismos, lo que se traduce en un decrecimiento continuo de sus concentraciones. Algunos ejemplos de este tipo de procesos son: la etapa de desinfección en el tratamiento de aguas potables o residuales (cloración, ozonización, rayos ultravioleta, etc .... ), las lagunas terciarias en los tratamientos de aguas residuales por lagunaje y la autodepuración que tienen lugar tras el vertido de un agua residual a un río, a un lago o al mar.

Al estudiar estos procesos con vistas al dimensionamiento del sistema de tratamiento, es muy habitual hacer la hipótesis de que, manteniendo las mismas condiciones ambientales, la disminución de concentraciones de un grupo determinado de microorganismos (por ejemplo, coliformes fecales, salmonelas o enterovirus) sigue una ley exponencial:

C(t) = C_o · e^-kt [1]

Son varias las razones que justifican el éxito de esta hipótesis a pesar de que, como se verá más adelante, los resultados experimentales muestran desviaciones sistemáticas respecto a dicha ley.

En primer lugar, se trata de una expresión muy sencilla que, aparte de la concentración inicial C_o , sólo depende de un parámetro (k).

Por otra parte, es una expresión que aparece en muchos campos de la ciencia y de la ingeniería, por lo que los usuarios suelen estar ya familiarizados con ella.

Una propiedad importante de la ley exponencial consiste en que a incrementos iguales de tiempo corresponden iguales disminuciones relativas de concentraciones, por lo que es habitual expresar la constante de la ley como el intervalo de tiempo necesario para que una concentración determinada se reduzca a la mitad (t_1/2) o a la décima parte (T₉₀) siendo éste último el que se utiliza en Ingeniería del Saneamiento. La relación entre k y estos intervalos de tiempo se deduce fácilmente por aplicación de [11] y resulta:

[2] [3]

Utilizando el parámetro T₉₀, la expresión [1] puede escribirse de otra forma más fácil de interpretar y, por ello, más utilizada:

C(t) = C_o ·10 ^{–t/ T90} [4]

Otra propiedad de gran utilidad práctica es que si se representa la expresión [4] en papel semilogarítmico resulta una línea recta, lo que facilita su ajuste por regresión lineal a los datos experimentales.

Para poner de manifiesto el fundamento teórico que subyace bajo la hipótesis de decrecimiento exponencial, podemos eliminar C_o entre [1] y su derivada, obteniéndose:

[5]

que indica que la velocidad de decrecimiento de las concentraciones es proporcional a la concentración que hay en cada instante, siendo k la constante de proporcionalidad.

Esta misma expresión la encontramos, por ejemplo, para describir la descomposición de moléculas con cinética de primer orden o la desintegración de núcleos radiactivos, lo que nos da una pista para interpretar k. En efecto, si escribimos [5] en la forma:

            [6]

vemos que el primer miembro puede interpretarse como la frecuencia relativa de muertes (o inactivaciones) de microorganismos en el tiempo dt, por lo que k representa la probabilidad que tiene cada individuo de la población de que se produzca su muerte en dicho intervalo de tiempo. Puesto que k es constante, se deduce que la ley exponencial [1] implica una probabilidad constante de eliminación para todos los microorganismos del grupo considerado a lo largo de todo el proceso.

Naturalmente, la constante k dependerá del proceso concreto de que se trate y para cada uno de estos, de un variado conjunto de fenómenos que, de forma simultánea, contribuyen a la disminución de concentraciones. En las referencias (1) a (5) se pueden encontrar buenas descripciones de dichos fenómenos para el tratamiento de aguas residuales por lagunaje y, en las referencias (6) a (9), una revisión muy completa de lo que se sabe respecto a la inactivación bacteriana en los vertidos al mar.

DESVIACIONES SISTEMÁTICAS RESPECTO A LA LEY DE DECECRECIMIENTO EXPONENCIAL

A pesar del éxito de la ley de decrecimiento exponencial, numerosos autores han destacado el hecho de que los resultados experimentales muestran desviaciones significativas y sistemáticas respecto a ella.

Por una parte se producen variaciones debidas a que las condiciones ambientales no son constantes, lo que significa que la probabilidad k varía con el tiempo. Esto es evidente, por ejemplo, en los estanques del tratamiento por lagunaje o en los cauces receptores de los vertidos como consecuencia de la variación en la intensidad de la irradiación solar, pero también se produce en experimentos de laboratorio al variar la concentraciones de nutrientes o de predadores. Por ejemplo, en la referencia (8) se describe cómo un aumento paralelo de la población de protozoos se tradujo en una intensificación de la tasa de disminución de la población de bacterias.

Estos fenómenos no constituyen estrictamente una violación de la ley exponencial sino mas bien un inconveniente para su aplicación práctica y no los vamos a tratar aquí. Diremos, no obstante, que si las variaciones son cíclicas (por ejemplo día-noche) y los resultados interesan a lo largo de un período que incluye varios ciclos, todavía se puede aplicar la ley exponencial si se consideran adecuadamente los efectos de los cielos.

Otras desviaciones están relacionadas con la falta de representatividad de la muestra (mezcla por difusión de «edades" distintas en la muestra, tamaño pequeño de la muestra en relación con el de los remolinos que producen la dispersión, etc .... ) y con las incertidumbres de los análisis microbiológicos. Tampoco estas desviaciones van a ser consideradas en el presente artículo.

Las variaciones que nos interesa destacar aquí son unas desviaciones sistemáticas que parecen indicar que, a medida que transcurre el tiempo, el decaimiento se hace más lento que lo que se deduciría de una ley exponencial.

Así, por ejemplo, en la figura 1, construída a partir de los datos que aparecen en la referencia (9), se ha representado en escala semilogarítmica la evolución temporal de las concentraciones de coliformes totales y de Escherichia coli obtenidas en un gran número de experiencias de seguimiento del vertido realizado por un emisario submarino situado cerca de Marsella (Francia). En cada experiencia se medía también la concentración de un trazador conservativo para poder calcular la dilución sufrida por el agua de la muestra y corregir así las concentraciones bacteriológicas obtenidas para eliminar el efecto de la dilución. Las concentraciones relativas que se representan en la figura se han calculado dividiendo estas concentraciones corregidas por la concentración medida en el instante inicial, justo encima del punto de vertido.   FIGURA 1. Concentraciones relativas de a) coliformes totales y b) Escherichia coli obtenidas en diferentes experiencias de seguimiento del efluente vertido por un emisario submarino situado en las proximidades de Marsella. (Gráficos preparados a partir de los datos de la referencia 9).

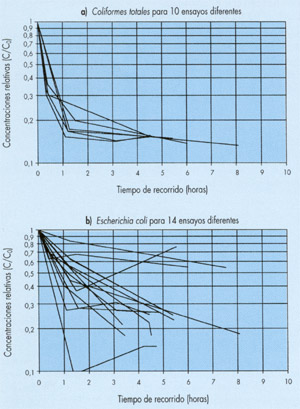Puede verse en dicha figura que en casi todos los casos la evolución de las concentraciones relativas viene representada por una curva de pendiente decreciente y no por una recta que es lo que correspondería a un decrecimiento exponencial.

Otro ejemplo lo vemos en la referencia (10) donde se dan las concentraciones de coliformes medidas en el entorno del emisario submarino de Ventura (California) a diferentes distancias del punto de vertido. El efecto de la desaparición bacteriana se calculó descontando el factor de dilución que se determinó midiendo también las concentraciones de un trazador conservativo (rodamina-B). En dicha referencia se propone como mejor ajuste de la tasa de desaparición una expresión del tipo:

        [7]

obteniéndose valores de las constantes dentro de los siguientes rangos: a entre 0.115 y 0.902, k₁ entre 0.078 y 1.94 h^-1 y k₂ entre 0.924 y 4.37 h^-1.

En la figura 2 se ha representado esta expresión en escala semilogarítmica para unos valores determinados de los parámetros. Puede comprobarse que el coeficiente instantáneo de desaparición bacteriana (valor de k en la expresión [5], que coincide con la derivada logarítmica de C(t) cambiada de signo y que está representado en este tipo de escala por la pendiente de la curva también con el signo cambiado, no es constante como correspondería a una ley exponencial simple, sino que comienza con un valor igual a a.k₁+(1-a). k₂ y va disminuyendo con el tiempo hasta estabilizarse en un valor igual al menor de los valores k₁ o k₂ (k₁ en el caso de la referencia (10)).

Como último ejemplo citaremos uno relacionado con el proceso de depuración en lagunas terciarias. Tras un gran número de medidas realizadas a lo largo de 15 años en Languedoc (Francia), se ha propuesto como expresión que mejor se ajusta a los resultados, la siguiente (ver referencia (1)):

[8]

donde t se expresa en días y k' toma valores entre 1,65 y 2,3 días ^-1/2 dependiendo del rango de variación de las temperaturas.

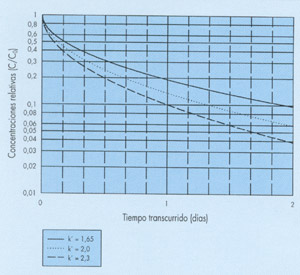
Esta ley de decrecimiento, que podríamos llamar exponencial-cuadrática para distinguirla de la exponencial-lineal [1], también depende de un solo parámetro (Y) y se representa en la figura 3 para varios valores de k'. Nótese que en

este caso el valor instantáneo de k es igual a , es decir, comienza siendo infinito y termina valiendo cero. También aquí se cumple la propiedad de que la tasa de disminución de las concentraciones se va haciendo cada vez más pequeña,

Las figuras 2 y 3 ilustran el hecho de que si se intenta ajustar globalmente una ley exponencial-lineal a un proceso del tipo doble-exponencial o exponencial-cuadrático, el valor de T₉₀ que se obtenga dependerá del intervalo de tiempo transcurrido entre la primera y la última muestra, siendo el resultado, en cualquier caso, poco representativo de la verdadera evolución de las concentraciones. La razón está en que el valor del parámetro T₉₀ sólo permanece constante para los procesos que siguen una ley exponencial-lineal y, por lo tanto, es un concepto que sólo tiene sentido para estos procesos.

FIGURA 2. Representación gráfica de la Ley doble-esponencial para distintos porcentajes de mezcla de dos subpoblaciones con valores de k iguales a 0.46 h-1 y a 2.3 h-1 , correspondientes a valores de T90 de 5 h y 1 h respectivamente.		FIGURA 3. Representación gráfica de la Ley exponencial-cuadrática C/C0=exp {-k'Öt} para distintos valores de k'(d-1/2}. Esta Ley fue deducida por el B.C.E.O.M. para representar el proceso de depuración en lagunas terciarias en la región de Languedoc (Francia) (Ref (1)).

PLANTEAMIENTO DE LA HIPÓTESIS DE POBLACIÓN INICIAL INFINITAMENTE SEGREGADA

La idea central de este artículo consiste en demostrar que una amplia variedad de curvas de decrecimiento pueden obtenerse suponiendo que en el instante inicial la población de microorganismos está compuesta por una distribución continua de subpoblaciones con distinta capacidad de supervivencia, pero manteniendo la hipótesis de que dentro de cada subpoblación, el decrecimiento sigue una ley exponencial-Iineal de parámetro k, para un cierto intervalo de valores que supondremos comprendido entre k = 0 (inmortal) hasta k = ¥ (muerte instantánea). Se trata pues, de ampliar la idea de segregación en dos subpoblaciones que llevó a la expresión [7] al caso general de segregación en infinitas subpoblaciones con distribución continua de valores de k.

Esta idea parece, en principio, bastante plausible pues, si bien en el caso de la descomposición de moléculas o en el de la desintegración de núcleos radiactivos puede suponerse que todos los elementos de la población inicial son iguales, siendo los procesos internos los que los hacen entrar con una cierta probabilidad (igual para todos) en un estado inestable, cuando se trata de seres vivos, cuya organización interna es mucho más compleja, que pueden tener orígenes distintos y que pueden encontrarse en distintas fases de su ciclo de vida, es lógico pensar que puedan existir subpoblaciones con distinta probabilidad de ser afectadas por las condiciones adversas.

No obstante, dentro de cada subpoblación deberán darse ciertas condiciones internas y externas al organismo para que se produzca la muerte de un individuo, lo que determinará el valor de la probabilidad k para esta subpoblación. El parámetro k representa, pues, la sensibilidad de la subpoblación a las condiciones adversas del medio.

Demostraremos a continuación que esta idea es también matemáticamente posible y deduciremos un procedimiento general para encontrar la composición inicial de una población en términos de su distribución porcentual respecto a los valores de k, a partir de una curva dada de decrecimiento de concentraciones.

TRATAMIENTO MATEMÁTICO. CONCEPTO DE FUNCIÓN DE REPARTO

Supondremos que se tiene una población inicial de C_o individuos en una unidad de volumen, distribuidos según los valores de su sensibilidad k de acuerdo con una cierta función de reparto inicial f_o (k). Esto quiere decir que el número de individuos con valores de k comprendidos entre k₁ y k₂ viene dado por:

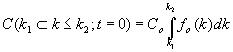[9]

La función f_o(k) no puede elegirse arbitrariamente, ya que debe cumplirse que

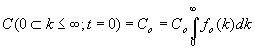[10]

de donde

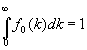[11]

O sea, el área encerrada entre su representación gráfica y el eje de abscisas debe ser igual a la unidad, lo que significa que la función de reparto f_o (k) puede tratarse como una función densidad de probabilidad.

La concentración de individuos de la subpoblación con sensibilidades comprendidas entre los valores k y k+ dk será C₀.f₀(k)·dk y evolucionará en el tiempo de acuerdo con una ley exponencial-lineal de parámetro k, de forma que en el instante t quedarán C_o·f_o(k) el dk individuos. Por lo tanto, la concentración total de individuos de todas las subpoblaciones en el instante t será:

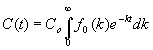[12]

y la función de reparto en el instante t será:

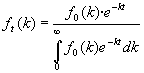[13]

que podemos imaginar que se obtiene a partir de f_o(k) suponiendo que cada ordenada decrece con el tiempo exponencialmente con parámetro igual a su abscisa (es decir, decrecen más rápidamente las ordenadas correspondientes a abscisas mayores) y dividiendo la función resultante por una constante (independiente de k, pero distinta para cada valor de t) para hacer que el área encerrada siga siendo la unidad y, por lo tanto, que dicha función de reparto sea en todo instante una función densidad de probabilidad.

La expresión [12] es fundamental en este nuevo enfoque porque nos permite calcular la curva de evolución de concentraciones a partir de una función de reparto inicial arbitraria. Además, se trata de una integral muy conocida en matemáticas. En efecto, escribiéndola en la forma:

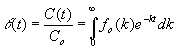[14]

se obtiene el importante resultado de que la función q (t), que representa cómo varían las concentraciones relativas a lo largo del tiempo, es la transformada de Laplace de la función de reparto inicial f_o(k).

Este resultado abre grandes posibilidades de aplicación del nuevo enfoque presentado en este artículo, ya que existe mucha bibliografía sobre la transformada de Laplace y se conocen un gran número de parejas función-transformada.

Para ilustrar cómo puede aplicarse este método vamos a obtener en primer lugar el resultado ya conocido de población inicial homogénea con parámetro k_o.

En este caso la función de reparto viene representada por la función generalizada delta de Dirac d (k-K_o) que, obviando el rigor de la teoría de distribuciones, se puede describir como una función que sólo existe en un entorno infinitamente pequeño de k = k₀ y que toma valores tan grandes que encierra un área de unidad. Es sabido que entonces se cumple:

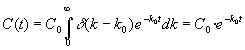[15]

es decir, se obtiene la ya conocida ley exponencial-lineal. Este mismo resultado se obtiene sabiendo que la transformada de Laplace de una delta de Dirac colocada en k = k₀ es e ^{– k}₀^t.

Del mismo modo, la ley doble-exponencial [7] corresponde a una función de reparto inicial:

f_o(k) = a - d (k – k₀) + (1- a) - d (k - k₂) [16]

que representa dos subpoblaciones de constantes k₁ y k₂ y de abundancias relativas iniciales a y (1 - a).

Este mismo procedimiento es aplicable a cualquier número finito de subpoblaciones con valores de k diferentes.

Veamos ahora el caso de la ley exponencial-cuadrática. A partir de la expresión [8] se obtiene:

[17]

y deseamos encontrar la función de reparto inicial que daría lugar a esta ley de variación de concentraciones relativas. En otras palabras, se trata de encontrar la transformada inversa de Laplace de [17]. Buscando en una tabla de transformadas se encuentra que dicha función es:

[18]

Puede comprobarse que [18] satisface la condición [11] para cualquier valor de k'

En la figura 4 se representan gráficamente los pares de funciones q (t) « f_o(k) para los tres casos mencionados: exponencial-lineal, doble-exponencial y exponencial-cuadrática.

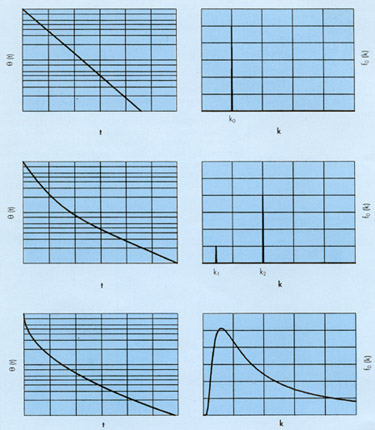FIGURA 4. Pares le de decrecimiento-función de reparto para los tres casos siguientes: arriba exponencial-lineal, en el centro ley doble-esponencial y debajo ley exponecial-cuadrática. Nótese que las funciones de reparto amplifican las leves diferencias existentes entre las diferentes leyes de crecimiento.

Nótese que las funciones de reparto presentan diferencias mucho más aparentes que las leyes de decrecimiento a corto plazo. No obstante, las diferencias entre éstas se hacen mucho más patentes a largo plazo y esta información se encuentra ya contenida en la función de reparto inicial.

En general, dada una curva q (t) de decrecimiento de concentraciones relativas, el procedimiento a seguir para obtener la función de reparto inicial asociada consiste en aproximar dicha curva mediante una función elemental de entre las muchas de las que se sabe que son transformadas de Laplace de otra, siendo entonces esta última la función de reparto buscada.

Sin embargo, conviene saber que existen ciertas limitaciones para la forma de las funciones q (t) que pueden ser transformadas de Laplace de alguna función de reparto f₀(k).

La primera se deduce observando que la condición [11] puede obtenerse de la expresión [14] haciendo en ésta t = 0, lo que significa que q (t=0) = 1.

Las demás se deducen de las conocidas propiedades de la transformada de Laplace:

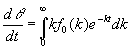[19]

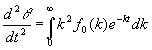[20]

En efecto, teniendo en cuenta que f_o(k) es una función que no puede tomar valores negativos, de [19] y [20] se obtienen respectivamente que dq /dt < 0 y que d^2q /dt² > 0 sea cual sea el valor de t. La primera de estas propiedades indica que las concentraciones relativas no pueden crecer en ningún momento, lo cual no es sorprendente, pero la segunda sí aporta información. Nos dice que la pendiente de la función q (t) ha de crecer en todo momento. Puesto que dicha pendiente es negativa, la tangente a la curva va tendiendo a ponerse horizontal a medida que crece t. De hecho, a partir de [19] se puede demostrar que el límite de dicha pendiente cuando t tiende a infinito es cero ¹, lo cual solo es una consecuencia de que entonces la población total ha desaparecido. 

OTRAS FUNCIONES DE REPARTO INICIAL

Las leyes exponencial-lineal y exponencial-cuadrática dependen de un sólo parámetro (k_o en la primera y k’ en la segunda), lo cual, si bien las hace más fáciles de manejar, puede representar un problema al tratar de ajustarlas a los datos experimentales, ya que sólo se dispone de un grado de libertad.

Por otra parte, la ley doble-exponencial depende de tres parámetros (k₁, k₂ y a), lo que hace que se requiera un elevado número de medidas para poder determinarlos con cierta fiabilidad.

En muchos casos puede ser más conveniente utilizar leyes que dependan de 2 parámetros con lo que atenuarán los problemas de las operaciones anteriores. Una de estas puede ser la que corresponde a la siguiente familia de funciones de reparto:

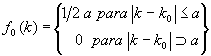[21]

lo que significa que sólo son posibles los valores de k que se diferencien de un valor dado k_o en una cantidad no mayor que a, siendo además todos ellos equiprobables.

La función de concentraciones relativas será en este caso:

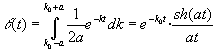[22]

FIGURA 5. Comparación de varias funciones de reparto de tipo rectangular con la Ley de decrecimiento exponencial-lineal con el mismo valor de k0 .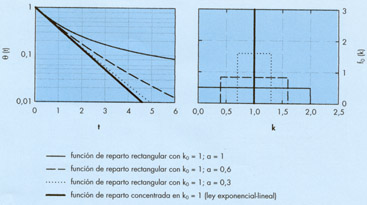

En la figura 5 se representan varios ejemplos de esta función de reparto uniforme correspondientes a un valor determinado de k_o y a varios valores del parámetro a. Obsérvese que cuando a tiende a cero, esta ley de reparto uniforme se convierte en la ley exponencial-lineal con el mismo valor de k_o. Además, el valor inicial de la derivada de la expresión [22] vale -k_o (independiente de a), lo que significa que este valor podría deducirse midiendo la pendiente en el origen de cualquiera de las curvas de concentraciones relativas. Por otro lado, el aspecto de estas curvas es muy parecido al de las curvas de la figura 4 correspondientes a otros modelos propuestos para aproximar resultados experimentales.

En el caso particular en el que a = k_o, la expresión [22] se simplifica convirtiéndose en:

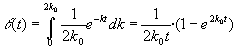[23]

que depende de un sólo parámetro (k_o), determinable como se ha visto antes por la pendiente en el origen. Una de las curvas de la figura 5 corresponde a este caso.

Ahora bien, la función de reparto inicial [21] no tiene la propiedad de ser autorreproducible, es decir, a medida que pasa el tiempo la función de reparto existente en cada instante tiene una expresión analítica de un tipo diferente al de la función de reparto inicial. Recordemos que de acuerdo con [13], la función de reparto instantánea f_t(k) se calcula multiplicando la inicial por e -^kt y dividiendo por una constante para que siga encerrando un área unidad. Por lo tanto, la ley exponencial-simple sí es autorreproducible (en toda instante la función de reparto sigue siendo una delta de Dirac) pero ni la exponencial-cuadrática ni la de reparto uniforme lo son porque al multiplicar [18] o [21] por e ^-kt cambia el tipo de expresión analítica.

LA FUNCIÓN DE REPARTO AUTORREPRODUCIBLE

Como no hay razón para pensar que el tipo de función de reparto en el instante en el que comenzamos las medidas tenga que ser diferente, parece lógico imponer que esta deba ser autorreproducible, es decir, que se mantenga el tipo de función aunque puedan variar los parámetros. Esto se consigue simplemente incluyendo en la función de reparto inicial una función exponencial del tipo e^-ak, puesto que al multiplicar por e ^-kt se obtendría e-^(a+t)k que es del mismo tipo. El parámetro a debe ser positivo para que la probabilidad de tener valores muy elevados de k vaya tendiendo a cero (ausencia de subpoblaciones sometidas a muerte instantánea). Para conseguir que tampoco existan subpoblaciones inmortales (M) se puede multiplicar la exponencial anterior por una potencia positiva cualquiera de k. Si además se tiene en cuenta que la función f_o(k) debe encerrar un área unidad obtenemos la siguiente función de reparto autorreproducible:

[24]

[24]

donde, en principio, el parámetro b ha de ser mayor que la unidad (más adelante se verá que también son admisibles los valores 0 < b <= 1).

Es fácil comprobar que la función de reparto en el instante t es:

[25]

es decir, el único cambio que experimenta la función de reparto a medida que transcurre el tiempo es un crecimiento del parámetro a en una cantidad igual al tiempo transcurrido.

La expresión [24] es muy conocida en Teoría de probabilidades porque representa la distribución gamma. El valor medio de k es b /a, la moda (valor de k para el cual la función de reparto toma un valor máximo) es (b-1) la y la desviación típica es Ö b/a. Por lo tanto, teniendo en cuenta [25] se demuestra que media, moda y desviación típica decrecen con el tiempo y tienden a cero cuando éste tiende a infinito.

El comportamiento de la función [24] para valores de k próximos a cero depende mucho de los valores del parámetro b. Cuando 0 < b < 1, la función tiende a infinito cuando k tiende a cero; cuando b = 1, toma el valor finito a cuando k = 0; cuando 1 < b < 2, la función se anula pero su derivada tiende a infinito ; cuando b = 2, la función se anula y la derivada toma el valor finito (b - 1); finalmente, cuando b > 2, tanto la función como la derivada se anulan en el origen. En la figura 6 se ha representado un ejemplo de cada uno de estos casos.

FIGURA 6. Comparación de varias funciones de reparto autorreproducibles correspondientes a distintos valores del parámetro b con a=1 en todos los casos. Nótese que la moda se encuentra siempre en k= b-1.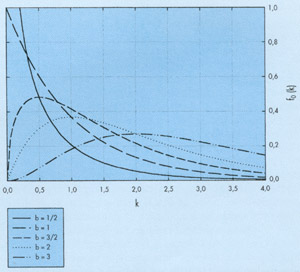

Por otra parte, usando la fórmula de Stirling es posible demostrar que cuando a y b tienden a infinito pero manteniéndose constante el cociente b/a = k_o, la expresión [24] tiende a la función delta de Dirac situada en k = k_o, de donde se deduce que la ley exponencial-lineal es también un caso particular de la función de reparto autorreproducible, o más exactamente, de la ley de decrecimiento asociada a dicha función de reparto.

Existe un precedente ilustre de función de reparto del tipo [24] en el campo de la Física. En efecto, en la teoría cinética de los gases juega un papel fundamental la ley de Maxwell de distribución de moléculas por velocidades

[26]

siendo dn_u el número de moléculas de un total de n que tienen velocidades comprendidas entre u y u+du, m es la masa de las moléculas, T la temperatura absoluta y k la constante de Boltzmann.

Si expresamos [26] en función de la energía cinética de las moléculas (E=mu² /2) se obtiene:

[27]

que es una función de reparto del tipo [24] con a = (kT)^-1 y b = 3/2 (la variable en este caso es E en lugar de k).

LEY DE DECRECIMIENTO ASOCIADA A LA FUNCIÓN DE REPARTO AUTORREPRODUCIBLE

Una vez justificada la adopción de una función de reparto aparentemente complicada como es la [24], estudiemos ahora su correspondiente ley de decrecimiento de concentraciones relativas.

Con ayuda de una tabla de transformadas de Laplace y usando algunas propiedades de la transformada inversa se obtiene que la función de concentraciones relativas es:

[28]

expresión que resulta sorprendentemente sencilla y que llamaremos ley hiperbólica de decrecimiento. Como comprobación observemos que el límite de esta expresión cuando a y b tienden a infinito de forma que se mantiene constante el cociente b /a = k_o resulta ser e ^–k0t, es decir, la ley exponencial-lineal, lo cual concuerda con la propiedad que se comentó antes.

Ahora podemos demostrar la afirmación que se hizo antes de que también eran admisibles los valores
0 <bÍ 1 a pesar de que en estos casos existe una fracción infinitésirna de la población que es "casi" inmortal. En efecto, la expresión [28] nos dice que si a es finito, la concentración relativa tiende a cero cuando t tiende a infinito para cualquier valor positivo de b.

Si hacemos el cambio de variable z = log  q , la ley hiperbólica puede escribirse en la forma:

[29]

Esto quiere decir que en un diagrama semilogarítmico, si fijamos b, las curvas que se obtienen de [29] al tomar diferentes valores de a son homotéticas en el sentido de las abscisas y su factor de homotecia es precisamente el parámetro a. Asimismo, fijando a, las curvas que se obtienen al variar b son homotéticas en el sentido de las ordenadas siendo su factor de homotecia el parámetro b. De hecho, si representáramos en abscisas la variable t/a y en ordenadas z/b todas las curvas colapsarían en una sola que es simplemente una curva logarítmica invertida con el eje de ordenadas situado en el punto donde ésta corta al eje de abscisas.

Por desgracia esto resulta poco útil en la práctica porque a prior¡ los valores de a y b son desconocidos. El cálculo de estos parámetros a partir de un conjunto experimental de parejas de valores (t_i, q _i) se hará en general mediante un ajuste por regresión no lineal utilizando cualquiera de los programas que existen en el mercado. No obstante, se describe a continuación un procedimiento aproximado que puede llevarse a cabo con ayuda de cualquier hoja de cálculo e incluso con una simple calculadora, y que sirve además para ilustrar el grado de flexibilidad que tiene la ley hiperbólica para ajustarse a conjuntos de datos experimentales.

Se comienza representando en un diagrama semilogarítmico las parejas de valores (t_i, q _i ). Se elige a continuación un punto por donde parezca claro que deba pasar la curva ajustada, preferiblemente para un valor de t próximo a la duración total del experimento (recordemos que el punto inicial de la curva es conocido: q = 1 para t = 0). Llamando (T, Q) a las coordenadas de este punto y Z = log Q , sustituyendo en [29] se obtiene:

[30]

con lo cual ya solo hay que ajustar el parámetro a.

Para ello se tantean unos pocos valores de a teniendo en cuenta que si a >> T (por ejemplo, a > 10 T) se obtiene una ley muy parecida a la exponencial-lineal y, por tanto, vendrá representada por una línea recta que une los dos puntos conocidos a saber: (0, 1) y (T, Q ). Por el contrario, si a >> T (por ejemplo, a < 10^-10 T) se obtiene algo parecido a los dos lados de un rectángulo, es decir, una curva que empieza descendiendo casi verticalmente hasta el entorno del punto (0, Q ) y que continúa casi horizontalmente hasta el punto (T, Q ). Las curvas correspondientes a los valores intermedios de a barren todo el espacio existente entre este semirrectángulo y su diagonal, lo que sirve de orientación para elegir los valores a utilizar en los tanteos. Concretamente, tomando a = T / 243, la curva pasa casi exactamente por el centro del triángulo de vértices (0, l), (0, Q ) y (T, Q ). El valor correspondiente de b sería entonces b=-0,42-log Q .

En la figura 7 se han representado un conjunto de leyes hiperbólicas de decrecimiento para las que se ha tomado como punto fijo de paso el que tiene de coordenadas Q = 10^-2 y T = 10h y en la figura 8 se representa el resultado de aplicar este método para un ajuste visual de los datos experimentales de la figura 1.

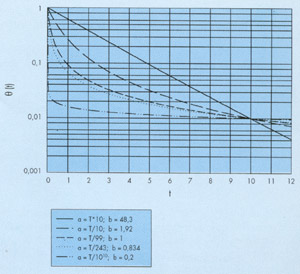FIGURA 7. Algunas leyes hiperbólicas de decrecimiento (asociadas a la función de reparto autorreproducible), calculados con la condición de que pasen por el punto fijo de coordenadas T=10 h y q=0.01.

FIGURA 8. Ajuste visual de una ley hiperbólica de decrecimiento a los datos representados en la figura 1 utilizando el método explicado en el texto. Se ha tomado como punto fijo T=8.08 h y Q= 0.133, último punto de la serie. Los valores obtenidos de los parámetros han sido a=T/2000=0.0040 y b=0.234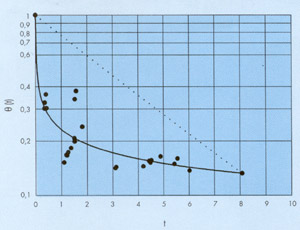

OTRAS HIPÓTESIS QUE CONDUCEN A LA LEY HIPERBÓLICA DE DECRECIMIENTO

La ley hiperbólica de decrecimiento, representada por la expresión [28], puede obtenerse también a partir de hipótesis diferentes de la de población infinitamente segregada.

Si eliminamos la variable t entre dicha expresión y su derivada respecto al tiempo obtenemos:

[31]

Esta ecuación diferencial, que por la forma en la que la hemos deducido expresa cuál es la tasa de decrecimiento para una población infinitamente segregada con una función de reparto inicial autorreproducible, también es la que correspondería a una población homogénea cuya tasa de decrecimiento fuera proporcional a la potencia (b+1)/b de la concentración instantánea q , siendo k = b/a la constante de proporcionalidad.

Puesto que b puede variar desde cero hasta infinito, el exponente varía entre infinito y la unidad. En este último caso la tasa de decrecimiento sería proporcional a la concentración, lo que, como se vio al principio de este artículo, constituye la hipótesis que conduce a la ley exponencial-Iineal. Esto representa una nueva comprobación del resultado ya conocido de que la ley exponencial-lineal es un caso particular de la ley hiperbólica cuando b y a tienden a infinito de tal forma que el cociente b /a = k_o se mantiene constante.

Cuando b = 1 se obtiene una tasa de decrecimiento proporcional al cuadrado de la concentración, hipótesis que se adopta con frecuencia en los modelos ecológicos para representar la competencia entre individuos de la misma especie para aprovechar los recursos escasos. Los modelos clásicos de Verhulst (ecuación logística), Lotka o Volterra incluyen un término como éste. Véanse por ejemplo las referencias (11) y (12).

La doble interpretación que acabamos de hacer de la ecuación [31], así como de la ley hiperbólica de decrecimiento es aplicable a cualquier ley de decrecimiento, es decir, dada una ley de decrecimiento, siempre es posible interpretarla como correspondiente a una población homogénea cuyos individuos tengan todos la misma capacidad de supervivencia, pero la misma ley puede corresponder a muchos tipos de poblaciones segregadas donde las distintas sulbpoblaciones tengan capacidades de supervivencia diferentes.

Mencionaremos para terminar otro caso en el que aparece una expresión similar a la ley hiperbólica de decrecimiento. Si el parámetro b es entero, la ley hiperbólica [28] corresponde también a la concentración relativa que se obtiene a la salida de b estanques de lagunaje iguales conectados en serie suponiendo que la población es homogénea con tasa de decrecimiento exponencial-lineal de parámetro k ₀ = 1 /a, siendo t = V/ Q el tiempo de retención en cada uno (V. volumen de cada estanque ; Q: caudal permanente que circula por los estanques). Ver referencia (2).

RESUMEN Y CONCLUSIONES

En los procesos de desinfección, se han venido proponiendo diversos modelos de leyes de decrecimiento de la población bacteriana para tener en cuenta las desviaciones sistemáticas que se obtienen experimentalmente respecto a la conocida ley exponencial-lineal. Ejemplos de éstas son la dobleexponencial y la exponencial-cuadrática, que se han deducido sobre una base puramente experimental.

En el presente artículo se propone una explicación de estas desviaciones basada en lo que hemos denominado hipótesis de población infinitamente segregada, que consiste en suponer que en el instante inicial la población de microorganismos está compuesta por una distribución continua de subpoblaciones con distinta capacidad de supervivencia, pero manteniendo la hipótesis de que dentro de cada subpoblación, el decrecimiento sigue una ley exponencial-lineal de parámetro k, para un cierto intervalo de valores que suponemos comprendido entre k = 0 (inmortal) hasta k = ¥ (muerte instantánea).

A partir de esta hipótesis se demuestra que la ley de decrecimiento de las concentraciones es la transformada de Laplace de la función de reparto inicial, lo que permite obtener una amplia gama de leyes de decrecimiento. En particular, todas las leyes propuestas están asociadas a las respectivas funciones de reparto que se calculan en el artículo.

Se propone una función de reparto inicial sobre la base de que sea autorreproducible, ya que no parece lógico que el tipo de función dependa del momento en que empecemos a hacer las medidas. Dicha función coincide con la distribución gamma de la Teoría de probabilidades, lo que nos ha permitido conocer rápidamente muchas de sus propiedades. Su transformada de Laplace nos da una ley de decrecimiento de tipo hiperbólico con dos parámetros que en general habrá que calcular por ajuste no lineal con los datos experimentales. No obstante, se dan algunas reglas y ejemplos que facilitarán dicho ajuste en la práctica.

Finalmente se comentan otras hipótesis que también conducen a la ley hiperbólica de decrecimiento.

(*) Licenciado en Biología. Departamento de Microbiología III. Facultad de Biología de la Universidad Complutense de Madrid.
(**) Ingeniero de Caminos, Canales y Puertos. Centro de Estudios de Puertos y Costas del CEDEX. Ministerio de Fomento

(1) Nótese que esto no implica que la pendiente de la representación en diagrama logarítmico (que coincide con la derivada logarítmica) tienda también a cero cuando t tiende a infinito, como se puede comprobar fácilmente en el caso de la ley exponencial-lineal.

	SUMARIO