|
||||||||||
|
Modelización hidráulica de caudales ecológicos |
LUIS DOCAMPO PÉREZ (*)
Palabras clave: Modelización Manning; Chézy; Moody; Hidráulica;
Caudal ecológico.
1. MODELOS DE CAUDALES ECOLÓGICOS
Con el comienzo de la década de los 90 se plantea en España la necesidad de establecer unos caudales circulantes que evitasen impactos negativos en los ecosistemas fluviales, y que al mismo tiempo permitiesen el aprovechamiento de las aguas para las centrales hidroeléctricas, embalses de abastecimiento, regadío, piscifactorias, etc. Para tal fin se empiezan a aplicar metodologías de distinta índole (clasificación hidrológica de los ríos, balances de masas o modelos de calidad fisicoquímica de las aguas fluviales, simulación hidráulica, análisis cronológicos de series de caudales, conservación y potenciación del hábitat fluvial para una o unas pocas especies de peces, conservación de la riqueza de especies biológicas - además de los peces -, etc.), que motivaron una amalgama de interpretaciones sobre los caudales ecológicos. Esta amalgama estaba motivada por los enfoques científicos de los distintos profesionales que participaban en el diseño y cálculo de los caudales ecológicos. Derivaron varios conceptos desde los distintos enfoques: caudal de dilución, caudal ecológico (mínimo) (óptimo) (aconsejable), caudal base, caudal de mantenimiento, caudal de compensación, caudal hidraúlico, etc. Todos ellos son igualmente validos para los fines con que fueron diseñados, pudiéndose englobar en un solo concepto de Caudal Ecológico (QE), definido como el mas lógico de los caudales que debe establecerse para cumplir una serie de criterios de gestión:
1. El Caudal Ecológico debe ser hidrológicamente coherente, es decir, tendrá que ser transportado de forma natural por el río (de acuerdo con los balances de precipitación-escorrentia) durante la mayor parte del periodo para el que se establezca, de tal manera que su cumplimiento no implique inyectar agua en el río a través de trasvases o sueltas de embalses.
2. El Caudal Ecológico debe ser variable, distinto según las épocas del año, y correlacionado con el hidrograma.
3. En los tramos que se encuentran en condiciones naturales, el QE debe potenciar la conservación de la fauna (invertebrados, peces, batracios, aves y mamíferos acuáticos), flora acuática y estructura del paisaje de las riberas. En estos casos hay que prestar especial atención a la calidad del hábitat de las especies endémicas, relictas o catalogadas como Vulnerables o en Peligro de Extinción (si las hubiera), sobre las especies destinadas a producción o a la pesca deportiva. Verbigracia, en tramos de algunos ríos vascos cohabitan dos especies piscícolas que son el espinoso (Gasterosteus aculeatus) y la trucha común (Salmo trutta m. fario) cuyos hábitats óptimos son incompatibles.
Podemos optimizar el hábitat de la trucha estableciendo caudales ecológicos que generen velocidades de corriente moderadamente altas (40 cm s-1 a 60 cm s-1) y temperaturas del agua moderadamente bajas (10º C a 15º C), lo que va en detrimento de las poblaciones de espinoso, cuya hábitat óptimo está caracterizado por menores velocidades de corriente (0 cm s-1 a 25 cm s-1) y mayores temperaturas (15º C a 18º C). G. aculeatus es una especie catalogada por el Decreto 167/1996 del País Vasco (B.O.P.V, núm. 140), como Vulnerable a la extinción; la Lista Roja de los Vertebrados de España del ICONA, también cataloga al espinoso como Vulnerable en todo el territorio nacional. Al mismo tiempo la Ley 16/1994 de Conservación de la Naturaleza del País Vasco (B.O.P.V, núm. 142), sanciona drásticamente la muerte, tenencia y/o degradación del hábitat de especies catalogadas como Vulnerables o En Peligro de extinción (multa de 10 a 50 millones de pesetas). Cuanto menos, los proyectos de caudales ecológicos promovidos por las administraciones competentes deberán priorizar la optimización del hábitat de especies catalogadas cuya destrucción o alteración se considera infracción muy grave, frente a las especies de uso recreativo o productivo, cuya alteración del medio se considera infracción leve o menos grave.
4. En tramos, ríos o cuencas contaminadas, donde la fauna (inclusive los peces), flora y paisaje, están reducidos a su mínima expresión como consecuencia de las cargas contaminantes, el caudal ecológico debe mejorar la calidad fisicoquímica de las aguas, más aun si existe la posibilidad de descargar aguas mediante un embalse de regulación. Es eternamente utópico pretender, en primer lugar, depurar todos los ríos (deseable si), y después establecer caudales ecológicos basados en criterios de potenciación del hábitat de la fauna y flora. En muchos ríos (p.ej. del País Vasco) estando en pleno funcionamiento los planes de saneamiento integral de cuencas, los tramos siguen mostrando mala calidad y un pésimo estado ecológico; aun habiéndose recuperado, la recuperación no alcanza unos valores mínimos establecidos en Directivas, Reales Decretos, legislación autonómica, etc. Los caudales de dilución basados en balances de masas de las sustancias implicadas, han sido muy criticados y menospreciados como caudales ecológicos. Tal proceder carece de justificación científica, ya que las variaciones de caudal implican variaciones en la química ( concentración de iones conservativos, oxígeno disuelto, compuestos nitrogenados, ortofosfato, ácidos húmicos y fúlvicos, etc.) y en la temperatura de las aguas, cuya influencia en el hábitat de las especies y en la propia dinámica de todo el ecosistema fluvial puede llegar a ser decisiva. En tramos o ríos contaminados de cuencas con embalses de regulación ya construidos para otros usos, el caudal de dilución puede ser un criterio practico de gran utilidad que cumpla la función de caudal ecológico. Sin embargo, no debe utilizarse el caudal ecológico corno un criterio que justifique la construcción de embalses.
Los principales modelos y métodos que se utilizan para la determinación de caudales ecológicos se resumen como sigue:
i) Resolución del Principado de Asturias (1988/01/21), Decreto Foral Navarro (1990/344), el Q10% (0,1 x Caudal Medio Aritmético Interanual) del MOPU (1980) y Ley 6/1992 de la Junta de Castilla y León, utilizan como método de cálculo del QE un porcentaje fijo (10%, 20%, etc.) del caudal medio interanual, o fórmulas donde intervienen los caudales clasificados (Q330, Q347, superados por 330 y 347 días al año, respectivamente). Estas estimas de caudal ecológico tienen el inconveniente de que el QE es un módulo único a establecer durante todo el año o casi todo el año, sin tener en cuenta el régimen fluvial fluctuante a lo largo del año y de los años, además generan baja calidad de hábitat para las poblaciones piscícolas y para la conservación y dinámica ecológica de las riberas.
ii) Modelo de Simulación Hidráulica de White (1976). En distintas secciones de un tramo establece la relación algebraica existente entre el perímetro mojado y el caudal circulante. A partir de esta relación, los caudales se establecen teniendo en cuenta las condiciones de freza, cría y migración de ciertas especies de peces.
iii) Modelo de biomasa de Wyorning (Binns, 1982). Consiste en un modelo de regresión múltiple sin interacciones entre las variables independientes, que relaciona la biomasa piscícola de salmónidos (Kg Ha-1) versus, caudal al final del estío, rango anual de caudal, temperatura del agua, concentración de nitrato (N03-), velocidad del agua, tipo de sustrato, cobertura, erosión en las orillas y anchura del cauce. Las variables independientes están codificadas en una escala de 0 a 4. Es de gran utilidad para la familia de los salmónidos de Wyoming, cuya extrapolación a otros estados, países y regiones biogeográficas no ha sido comprobada.
iv) Modelo IFIM (Instream Flow Incremental Methodology) (su programación informática se denomina PHABSIM), desarrollado por el Servicio de Pesca y Vida Silvestre de los Estados Unidos (Bovee, 1982). Establece mediante simulación hidráulica curvas que relacionan el caudal circulante con la denominada Anchura Ponderada útil (APU). La APU es el producto de la anchura real del cauce por un coeficiente de ponderación, estimado de acuerdo con los siguientes parárnetros: profundidad del agua, velocidad del flujo, cobertura, sustrato y temperatura. La temperatura se considera constante al variar el caudal, lo que difiere de las estimaciones resultantes de la aplicación de la ecuación fundamental del transporte de masas en ríos, donde la tasa de incremento de calor por unidad de volumen de agua depende del caudal y de la profundidad hidráulica (área mojada/anchura mojada del cauce) (véase p.ej. Brown & BarnweIl, 1987). El IFIM se aplica con algunas especies de peces, en ningún caso se ha mostrado en la bibliografía consultada una aplicación con invertebrados del bentos fluvial, plantas acuáticas, anfibios u otros grupos taxonómicos. Los coeficientes de ponderación se determinan a partir de curvas de preferencia del hábitat de las especies de peces analizadas con respecto a los cinco parámetros indicados. Estas curvas resultan de ajustar polinomios de grado entero 3 o 4 a los histogramas de frecuencias de ocurrencia acumuladas de la especie para el parámetro considerado. La primera derivada de la curva polinómica ajustada, normalizada a la unidad, determina la curva de preferencia para ese parámetro. Normalmente IFIM se aplica estableciendo una ecuación de regresión lineal simple (potencial, exponencial o línea recta) entre la biomasa de la especie piscícola y la APU (García de Jalón, 1990). El caudal ecológico es aquel que genera una APU capaz de mantener una determina biomasa piscícola establecida previamente. Da lugar a valores de caudales ecológicos que no se ajustan al hidrograma de los ríos.
v) Modelo de medias móviles de Palau (1994). Aplica medias móviles sin transformar ni diferenciar, sobre la serie de caudales aforados o simulados de un tramo fluvial o río, para determinar los caudales ecológicos, los cuales posteriormente se ensayan mediante modelización hidráulica, y con las citadas curvas de preferencia de hábitats. El modelo en si constituye la parte más elemental de la metodología estadística utilizada para realizar análisis cronológicos (series temporales) de cualquier variable, denominada ARIMA (Proceso Autorregresivo Integrado de Media Móvil). Utiliza las medias móviles como tal, no establece autorregresiones, ni transformaciones, ni diferenciaciones con operadores de retardo, por lo que puede conducir a resultados contradictorios, ciclos irreales, funciones crecientes de forma monótona, etc. (Box & Jenkins, 1976; Spiegel, 1993; Peña, 1989).
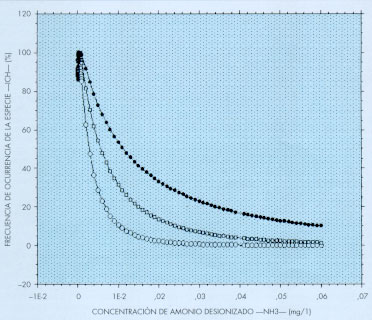
vi) Balances de Masas. Los modelos de predicción de las características fisicoquímicas de las aguas basados en la ecuación general del balance de masas (transporte, dispersión, dilución, sumideros y reacciones químicas), como el QUAL 2E (Brown & Barnwell, 1987), MICHRIV model (Delos et al., 1983), etc., son de gran utilidad practica para determinar caudales ecológicos en ríos afectados por la contaminación y regulados por embalses. No existe ninguna característica fisicoquímica de las aguas fluviales que no fluctúe en función del caudal, y ninguno de los modelos anteriormente citados, excepto el de biomasa de Wyoming, utiliza parametros químicos de las aguas. De la misma forma que se manifiestan curvas de preferencia del hábitat de los peces u otros organismos frente a la velocidad de corriente o a la temperatura, también son ajustables curvas de preferencia respecto a otros parámetros como el oxígeno disuelto, nitrito (N02-), calcio (Ca2+), NH3, etc. (figura 1).
 |
|
La Propuesta de la Directiva Marco para la Protección de las Aguas Superficiales
y Subterráneas de la Unión Europea (1997) establece en su Anexo III la necesidad
de desarrollar por parte de los estados miembros, las especificaciones técnicas
que determinen volúmenes de captación en cualquier sistema acuático (río, ría,
lago, laguna, embalse, acuífero, ... ), para agua potable, uso agrícola, uso
industrial, etc. Es decir, el concepto de caudal ecológico hay que extrapolarlo
a otros ecosistemas que no sean las aguas fluyentes; en lagos, lagunas, acuíferos,
etc. hay que determinar volúmenes de captación, y en estos casos el uso de los
modelos de calidad fisicoquímica de las aguas, de forma independiente (p.ej.
en aguas subterráneas) o en correlación con las variables bióticas (p.ej. en
lagunas), van a ser imprescindibles.
vii) Método Vasco (Docampo & G. de Bikuña, 1995). Método elaborado para los ríos de la Comunidad Autónoma del País Vasco. Basado en la teoría biogeográfica insular de MacArthur & Wilson (1967), utiliza la modelización hidráulica y una curva de regresión de la riqueza de especies de invertebrados del bentos en función del perímetro mojado y del grado de irregularidad del cauce. Sin embargo, esta curva de regresión es poco determinista, ya que el coeficiente de determinación de Pearson r 2 = 0,794, y un 20% de la variabilidad de la biodiversidad de invertebrados fluviales no es explicada por la ecuación ajustada. El método da lugar a unos caudales ecológicos que se estiman como un porcentaje del caudal medio geométrico interanual, que no es aconsejable aplicar a otros ríos de otras regiones geográficas, donde seria recomendable ajustar todo el método. El ajuste del método resulta ser muy laborioso y tedioso, y sus resultados son módulos no correlacionados con las fluctuaciones del hidrograma natural de los ríos.
viii) Modelo RECE (Régimen Estacional de Caudales Ecológicos). Elaborado por el autor de este trabajo (Docampo, 1997). Este modelo procede de la siguiente forma:
1) Determinación del período mínimo para el cual deben estimarse los caudales ecológicos (cada mes, época del año, etc..) y Ajuste de la función de distribución estadística de la serie de caudales aforados o simulados del periodo considerado.
2) Cálculo del Caudal de Cambio mediante el primer punto de inflexión no nulo de la curva que ajusta la función de distribución de caudales. Este caudal de cambio esta destinado a ser el caudal ecológico de cada periodo, si cumple una serie de criterios biológicos (conservacionistas) y fisicoquímicos.
3) Modelización Hidráulica que permite establecer la relación entre la hidrología (caudal de cambio) y las características fisicoquímicas y biológicas del ecosistema fluvial.
4) Comprobación del cumplimiento de criterios abióticos y biológicos, entre los que destacan:
a) vulnerabilidad hidráulica de los cauces a la continuidad del flujo, derivada de la detracción de aguas.
b) irrigación de la vegetación de riberas (conservación del bosque de galería).
c) conservación de la biodiversidad fluvial, estimada como riqueza de especies de invertebrados del bentos, peces y batracios y
d) Indice de Calidad del Hábitat (ICH) de especies biológicas catalogadas o emblematicas, si las hubiese. El ICH es la frecuencia o probabilidad de ocurrencia de una especie (o conjunto de especies) frente a un valor de una variable fisicoquímica (figura l), y es equivalente a las curvas de preferencia del hábitat del modelo IFIM, de las cuales difiere en dos aspectos fundamentales:
1. El ICH se establece no solamente para las variables físicas del cauce (temperatura, calado, velocidad, coberturas, ... ) como lo hace el modelo IFIM, sino también para parámetros químicos (02, Ca 2+, N02-, NH3, ...) etc. (figuras 1 y 5).
2. Las curvas de ICH no se obtienen mediante regresión polinómica como en el modelo IFIM, si no aplicando el método estadístico de la máxima verosimilitud a la familia de transformaciones de Box - Cox, 1962, que normaliza la función de distribución de frecuencias acumuladas, y tomando como ecuación universal de la integral de la curva de Gauss la publicada en la revista del Ingeniería Civil número 103 (Docampo, 1996). De esta forma se evita que las ecuaciones del ICH o de la preferencia del hábitat de las especies, den lugar a resultados paradógicos (frecuencias de ocurrencia de las especies con valores negativos, infinitos o números imaginarios basados en i = Ö-1), como sucede en algunas aplicaciones informáticas del modelo IFIM.
Casi todos los métodos y modelos de determinación de caudales ecológicos anteriormente citados utilizan como una de sus partes fundamentales la simulación hidráulica, para relacionar los aspectos físicos y/o químicos de los cauces con sus características biológicas (índices de calidad del hábitat de especies catalogadas, biomasa piscícola, biodiversidad, etc.). En todos ellos esta simulación se basa en la ecuación de la velocidad media de corriente de Manning para régimen uniforme: V = (1/n) S0.5 Rh2/3, donde V es la velocidad media del agua en m s-1, "n" es el coeficiente de rugosidad del canal, S la pendiente de la linea de energía y Rh el radio hidráulico. Sin embargo, la aplicación de la ecuación de Manning no siempre es lo más adecuado en los cursos fluviales o cauces naturales, en lo que a su determinismo se refiere. El objetivo de este trabajo es demostrar, mediante una de las principales aplicaciones de la ecuación de Marming en ríos, la modelización hidráulica de caudales ecológicos, que existen muchos casos en los que las estimas de la velocidad de corriente y del caudal circulante realizadas con dicha ecuación difieren substancialmente de los valores reales. Para llevar a cabo este objetivo se propone la aplicación del modelo hidráulico I.H.R.A. (Ingeniería Hidráulica de Ríos y Acequias) a los ríos Llobregat y su afluente el Cardener, tal y como se describe en el siguiente apartado.
El modelo IHRA (Docampo, 1998a) plantea una modelización hidráulica generalista, tanto para el flujo uniforme como para el lentamente variable en canales abiertos, con o sin transporte de solidos suspendidos, donde la ecuación de Manning es un caso particular de dicha modelización. La aplicación de la ecuación de Manning solamente es viable cuando la rugosidad relativa del canal abierto adquiere valores comprendidos en un determinado rango intermedio: 0,001 < e /Dh < 0,05, donde E es la altura de la rugosidad y Dh es el diámetro hidráulico (véase por ejemplo White, 1988): Dh = 4 Rh. Fuera de este rango, es decir, para rugosidades bajas del canal (e/Dh < 0,001) o altas (e/Dh > 0,05), la ecuación de velocidad de corriente de Manning siempre predice caudales muy distintos de los que circulan por el canal, observándose errores (supravaloraciones del caudal) que superan el 20%, que en algunos casos prácticos han llegado a ser de hasta el 60%.
Los canales artificiales (de escollera, tierra, hormigón, gaviones, ... ) normalmente se diseñan dentro del citado rango de rugosidades intermedias, por lo que es viable la ecuación de Manning en cuanto a su determinismo se refiere, sin embargo, los ríos y demás cursos naturales (también en canales artificiales desgastados o alterados por la erosión), su rugosidad se encuentra fuera de este intervalo intermedio, observándose cauces en los que la rugosidad es alta y otros en los que es baja. En estos casos la ecuación de Manning conduce a resultados poco deterministas; la falta de precisión de la fórmula no es atribuible a una mala elección del coeficiente de rugosidad "n" de Manning del canal, ya que éste se determina de forma empinca mediante levantamientos hidráulicos de perfiles de velocidad, tal y como se describe más adelante.
La ecuación de velocidad de corriente de Manning es un caso particular de la ecuación de velocidad de Chézy, y ésta es a su vez un caso particular de la formulación del coeficiente de fricción del canal desarrollada a partir del diagrama de Moody (1944), y el diagrama de Moody es la base de toda la Mecánica experimental de fluidos, sean éstos líquidos o gases, sean estos transportados por tuberías cerradas o canales abiertos, si bien con las pertinentes modificaciones en cada caso (en White, 1988). Normalmente, las ecuaciones de Manning y Chézy se igual entre sí, estableciéndose una equivalencia entre el coeficiente de resistencia del canal C de Chézy y la "n" de Manning: C = (1/n) Rh1/6, tal proceder solamente es correcto en el mencionado rango de rugosidades relativas del canal. La innovación que introduce el modelo 1HRA es una modelización hidráulica general desarrollada a partir del coeficiente de fricción del canal, de tal manera que se pueden discriminar aquellas situaciones o canales en los que la fórmula de Manning es inviable por su gran indeterminismo. Cuando la aplicación de la ecuación de Manning es óptima, IHRA aporta la posibilidad de poder continuar la modelización hidráulica basada en esta ecuación, o bien continuar con la posibilidad general de una modelización desarrollada a partir del diagrama de Moody (formulación basada en el coeficiente de fricción del canal y en el número de Reyno1ds). La formulación del coeficiente de fricción es valida para todos los casos, sean canales artificiales o naturales, sean canales muy rugosos, poco rugosos o de rugosidades intermedias.
El modelo IHRA consta de los siguientes 8 componentes, donde se especifican ecuaciones que se utilizan en el presente trabajo:
![]() (1)
(1)
Clasificación del Régimen Hidrodínámico del Río o Acequia. Utiliza los números de Froude (Fr) y Reynolds (Re). SI Fr <= 1, los siguientes componentes (2), (3) y (4) carecen de fiabilidad y no son ejecutables. El modelo salta al componente (5). El número de Reynolds interviene en los componentes (2) y (3) y el de Froude lo hace en los componentes (5) y (7). Las fórmulas de los números de Froude (Fr) y Reynolds (Re) son respectivamente:
Re = V Rh/v (2)
V es la velocidad media de la corriente en m s-1, g = 9,81 m s-2 , D la profundidad hidráulica, a el coeficiente de energía o coeficiente de Coriolis, v el coeficiente de viscosidad cinemática del agua. a se determina empiricamente a partir del levantamiento hidráulico de velocidades de corriente en cada sección transversal, siendo a = ò u3 dA/(V3A), donde dA es el área mojada de cada franja de subdivisión de la sección transversal del cauce, u la velocidad media de cada una de estas franjas y V la velocidad media de toda la sección. El coeficiente de viscosidad cinemática M de las aguas de las estaciones de muestreo se ha determinado mediante una ecuación del modelo CEFA (Conjunto de Ecuaciones Fisicoquímicas del Agua) (Docampo, 1998b). La ecuación de v de este modelo estima la viscosidad cinemática del agua con un error máximo del 0,4%, mediante una ecuación de regresión múltiple de dos variables: la salinidad, que incrementa linealmente la viscosidad, y la temperatura, la cual produce un efecto de disminución exponencial de tercer grado, sobre la misma. En un río se considera que la presión hidrostática no tiene un efecto significativo sobre las variaciones de la viscosidad.
(2) Determinación Experimental del Coeficiente de Resistencia del Canal (la C de Chézy). El coeficiente de resistencia del canal de Chézy (C) en un río no se adopta a partir de los valores contenidos en las tablas (lo mismo que en el caso de la n de Manning), sino que se determina empiricamente a partir de la ley universal de distribución (logarítmica) de velocidad de Pradtl-Von Karman (Von Karman, 1930), siguiendo el método de medidas de velocidades en dos puntos de cada vertical de la sección húmeda, descrito en Chow (1990). IHRA incorpora sendas fórmulas empincas para controlar la variación de la C de Chézy y la "n" de Manníng en función de la profundidad del agua.
Aplicación de la Ecuación de Moody (Clasificación de la Rugosidad del Canal). La ecuación general de la velocidad media del régimen uniforme en canal abierto es V = C Rhx Sy donde "x" e "y" son exponentes empíricos. La ecuación de Manning es un caso particular de la misma, siendo C = l/n, "x" = 2/3 y "y" = 1/2. La ecuación de Chézy es otro caso particular pero un tanto más generalista, ya que responde a una deducción física o dimensional (balance de fuerzas), teniendo en cuenta la fuerza de resistencia de las paredes del canal y la turbulencia derivada de las fuerzas viscosas. Por el contrario, la ecuación de Manning es dimensional ni ente no homogénea, no responde a una interpretación física coherente, "n" se considera adimensional pero tiene las desconcertantes unidades de m1/3 s-1, corno consecuencia de que su deducción es puramente empírica, y en consecuencia su validez se limita al rango de datos con los que fue establecida, que no abarca todas las situaciones posibles existentes, especialmente en ríos naturales. La ecuación de velocidad de corriente de Chézy se expresa explícitamente corno sigue:
V = (8g/f)0.5 (Rh S)0.5 (3)
Donde todos los factores son conocidos, excepto "f', que es el coeficiente de fricción del canal, que puede calcularse mediante la C de Chézy estimada mediante el procedimiento descrito en el anterior componente:
f= Sg/C2 (4)
A partir de la estima del coeficiente de fricción "f" se determina la altura de la rugosidad del canal (e) mediante la ecuación de Colebrook (1939), dibujada posteriormente por Moody (1944) y cuyo diagrama constituye la base de la mecánica experimental de fluídos:
f -0.5 = -2 log[(e/3,7 Dh) + (2,51 f-0.5/Re)] (5)
Todos los términos de esta ecuación son conocidos, debiendo resolverse iterativamente, exceptuando los casos en los que el número de Reyno1ds (Re) es muy alto, en los que la ecuación puede expresarse de forma explícita. La relación entre la altura de la rugosidad y el diámetro hidráulico (e /Dh) permite analizar la validez de la modelización hidráulica realizada con la ecuación de Manning frente a la basada en la fórmula de Chézy.
Modelización Hidráulica. Por un lado, el modelo IHRA procede al ajuste de la formulación basada en el coeficiente de fricción del canal (f), y por otro, al de la ecuación de Manning, y compara entre ambos. Se selecciona el mejor ajuste de la velocidad media del flujo para proceder a la modelización hidráulica. Esta consiste en relacionar el caudal potencial o real que circula por el canal con el calado máximo (Q = f (H)), radio hidraúlico (Q = f(Rh)), perímetro mojado (Q = f(P)) y anchura mojada (Q = f(a)), entre otras relaciones posibles. En canales poco profundos las dos últimas relaciones son equivalentes. La modelización hidráulica permite traducir cualquier módulo de caudal en dimensiones geométricas y de velocidad, y a la inversa. Representa al componente del modelo IHRA de mayor aplicación interdisciplinaria, por ejemplo, para el cálculo de caudales ecológicos, cálculo de niveles de avenida, procesos de regeneración biológica de ríos, módulos de restauración ecológica de cauces y riberas, estima de parámetros utilizados en modelos de calidad fisicoquímica de las aguas como en el caso del QUAL 2E, etc. En este sentido, IHRA incorpora fórmulas para la determinación hidráulica del coeficiente de dispersión longitudinal de sustancias contaminantes (DL) y del coeficiente de reaireación o reoxigenación atmosférica (K2) del balance del oxígeno disuelto en las aguas fluviales.
(5) Vulnerabilidad Hidráulica y Estabilidad del Flujo. La Vulnerabilidad Hidráulica (VH) es un parámetro de gran utilidad ambiental; representa la facilidad con que un cauce hidráulicamente ancho se transforma en estrecho, y viceversa, ante la extracción o adición de caudales. Este componente determina que cauces pueden aproximarse de forma trapezoidal o de forma rectangular y cuales son muy irregulares. Asimismo, la VH interviene en el cálculo de la estabilidad del flujo de gran importancia en la previsión de catástrofes de índole fluvial. La Vulnerabilidad Hidráulica (VH) se estima mediante las siguientes fórmulas:
VH = 1 - k (6)
k = 1 - Rh (dP/dA) (7)
K es el coeficiente mórfico del número de Vedernikov. Rh, radio hidráulico y (dP/dA) es la primera derivada de la relación existente entre el perímetro mojado y el área mojada de la sección transversal del cauce. La VH constituye un parámetro utilizado en el cálculo de caudales ecológicos para el criterio de conservación del paisaje fluvial.
(6) Cálculo de la Capa Limite de un Vertedero o de un Canal. Permite determinar a que distancia de la entrada de un vertedero, canal de contorno, acequia de riego o confluencia de ríos, es aconsejable establecer estaciones de aforos, realizar medidas mecánicas de caudales y velocidades o tomar muestras de agua para su analítica fisicoquímica.
(7) Valores Críticos. Determina la profundidad critica, pendiente critica y velocidad critica en canales de sección rectangular y de sección no rectangular, de régimen uniforme o lentamente variable. Valores estos que son de gran importancia en el diseño de las canalizaciones fluviales. El cálculo de los valores críticos se realiza mediante dos rutas: a) formulación del coeficiente de fricción del canal y b) ecuación de Manning. Compara los resultados de ambas rutas, determinando la influencia de la rugosidad del material seleccionado para la construcción de la solera del canal, y corrigiendo los posibles defectos derivados de la no adecuación de la fórmula de Manning.
(8) Diseño de Secciones Hidráulicas Estables en canales no erosionables y en canales erosionables. En estos últimos, se determina para un caudal dado (Q) (correspondiente a un determinado periodo de retorno, a la descarga de un embalse o a cualquier módulo hidrológico), la sección hidráulica que no experimentara erosión y/o socavación de la solera como consecuencia de la fuerza tractiva o fuerza de arrastre de materiales no cohesivos suspendidos en el agua o rodantes sobre la solera. La sección hidráulica estable es determinada de acuerdo con la metodología recomendada por la U.S.Bureau Of Reclamation ( Glover & Florey, 1951). Si bien, el modelo IHRA incorpora en sus cálculos además de la formulación de Manning, la formulación del coeficiente de fricción o ecuación de Moody.
Los cinco primeros componentes del modelo IHRA se utilizan en la modelización hidráulica de caudales ecológicos, como la que se ensaya en este artículo. El ensayo se ha realizado en 7 tramos del río Llobregat y en 3 de su principal afluente el Cercenar. En estos 10 tramos se dispone de caudales aforados por limnígrafos en estaciones de aforos de la Junta D'Aigües de la Generalitat de Catalunya, donde se encuentra descrita la información pertinente sobre la descripción de los tramos, localización cartográfica , calidad del agua, estima de caudales ecológicos, etc. (Junta D'Aigües, 1996). Al mismo tiempo, se han realizado aforos mecánicos de los caudales circulantes en junio de 1995, utilizando los levantamientos hidraulicos recomendados por la U.S. Geological Survey (UN, 1954), en la que cada sección transversal del cauce se divide en varias franjas verticales. En cada vertical se mide la velocidad del flujo mediante un molinete de precisión, a (0,2 h) y (0,8 h), siendo "h" la profundidad de la lamina de agua en cada vertical. La velocidad media en cada vertical es el promedio de las velocidades tomadas a (0,2 h ) y (0,8 h). La velocidad media de todo el flujo se determina dividiendo la suma de caudales elementales de cada franja (Qi) entre el área total de la sección mojada (A): V = å Qi/A . Estos levantamientos hidraulicos son también utilizados para ajustar las ecuaciones de Manning y Chézy de acuerdo con la metodología descrita en los componentes (1), (2), (3) y (4) del modelo IHRA, descrita arriba.
Por un lado, en los citados tramos de los ríos Llobregat y Cardener, se hace una comparación de los caudales que se estiman con las fórmulas de Manning y Chézy con respecto al caudal circulante aforado por las estaciones de aforo en el día en el que se realizaron los levantamientos hidráulicos. Por otro, se procede a un cálculo de caudales ecológicos mediante modelización hidráulica, comparando las fórmulas de Manning y Chézy, en los tramos LL-53 (El Collet d'Eina) y La Coromina (C-42).
3. 1. COMPARACIÓN DE CAUDALES AFORADOS Y ESTIMADOS CON LAS FÓRMULAS DE MANNING Y CHÉZY
| ESTACIÓN | LOCALIDAD | Temperatura (ºC) | Viscosidad (centistokes) | Velocidad (ms-1) | Area (m2) | Reynolds (RE) | Froude (Fr) | a |
| LL-56 | La Pobla de Lillet | 12.50 | 1.222 | 0.484 | 2.886 | 130.059 | 0.320 | 1.417 |
| LL-53 | El Collet d´Eina | 12.50 | 1.222 | 0.485 | 3.507 | 181.100 | 0.273 | 1.502 |
| LL-60 | Colònia Rosal | 17.40 | 1.074 | 0.595 | 4.802 | 209.515 | 0.377 | 1.498 |
| LL-68 | Balsanery | 14.80 | 1.149 | 0.345 | 11.848 | 121.683 | 0.222 | 1.707 |
| LL-102 | Pont de Vilumara | 14.80 | 1.149 | 0.238 | 1.306 | 64.765 | 0.154 | 1.451 |
| LL-97 | Castellbell | 20.00 | 1.007 | 1.127 | 13.480 | 437.271 | 0.603 | 1.000 |
| LL-91 | Martorell | 19.20 | 1.027 | 0.874 | 12.906 | 452.187 | 0.382 | 1.117 |
| C-42 | La Coromina | 15.30 | 1.134 | 0.520 | 4.240 | 203.651 | 0.267 | 1.165 |
| C-39 | Súria | 16.30 | 1.105 | 0.392 | 7.702 | 166.620 | 0.170 | 0.921 |
| C-100 | Castellgalí | 16.00 | 1.113 | 0.847 | 5.450 | 229.623 | 0.523 | 1.129 |
![]()
TABLA 1. Características hidrodinámicas
de los tramos del río Llobragat (indicados por la letra LL) y su afluente el Cardener
(letra C) en la primavera de 1995. El coeficiente de viscosidad cinemática (n) es
centistokes ( 1 stoke= 1 cm2 s-1 ) se ha determinado mediante una
ecuación del modelo CEFA, y los números de Reynolds (RE) y Froude (Fr) se han calculado
con las ecuaciones (1) y (2), respectivamente. a,coeficiente de
distribución de la velocidad o coeficiente de Coriolis, utilizado en el cálculo Fr, y
computado con la fórmula a = òu3dA/(V3 A) especificada en la
descripción del modelo IHRA.
En la Tabla 1 se indican las principales características hidrodinámicas de los tramos analizados. Todos los regímenes fluviales son turbulentos y suberíticos. Señalamos que los tramos LL-97 (Castellbell) y C-39 (Súria) son estaciones de aforos constituidas por canales rectangulares de hormigón. En los tramos LL-53, LL-68, LL-102 y C-39 con números de Reynolds (Re) inferiores a 200.000, el cálculo de la altura de la rugosidad (e) debe realizarse iterando la fórmula de Moody (ecuación 5), en los demás tramos el efecto de Re es poco significativo, expresándose e en función del coeficiente de fricción del canal (f). Se han obtenido valores del coeficiente de Coriolis (a) entre aproximadamente 1 (canales rectangulares de hormigón de las estaciones de aforos LL-97 y C-39) y 1,71 (cauce natural muy irregular de la estación LL-68), similares a los aconsejados en otros trabajos (King, 1954; Kolupaila, 1956), donde a varia entre 1 en cauces regulares y 2 en cauces naturales y torrentes.
| ESTACIÓN | Rh(m) | S tanto por uno | e (mm) | e/Dh adimensional | f adimensional | n-Manning | C-Chézy |
| LL-56 | 0.328 | 0.001622 | 317 | 0.24150 | 0.177950 | 0.032 | 21.00 |
| LL-53 | 0.457 | 0.00127 | 494 | 0.27049 | 0.193707 | 0.034 | 20.128 |
| LL-60 | 0.378 | 0.00115 | 129 | 0.08536 | 0.093300 | 0.027 | 29.000 |
| LL-68 | 0.405 | 0.001397 | 909 | 0.56115 | 0.372599 | 0.038 | 14.513 |
| LL-102 | 0.312 | 0.000337 | 226 | 0.18103 | 0.145578 | 0.030 | 23.218 |
| LL-97 | 0.391 | 0.000910 | 2 | 0.00157 | 0.021982 | 0.014 | 59.752 |
| LL-91 | 0.531 | 0.003171 | 494 | 0.23251 | 0.173103 | 0.034 | 21.293 |
| C-42 | 0.444 | 0.000147 | 2 | 0.00087 | 0.019000 | 0.013 | 64.280 |
| C-39 | 0.469 | 0.000087 | 2 | 0.00131 | 0.020977 | 0.014 | 61.165 |
| C-100 | 0.302 | 0.000424 | 0.3 | 0.00022 | 0.014000 | 0.009684 | 74.860 |
TABLA 2. Características hidráulicas de los tramos analizados en los ríos
Llobregat (LL) y Cardener (C). Rh, redio hidráulico. S, pendiente de la línea de
energía. e, altura de la rugosidad del canal. e/Dh, rugosidad relativa. Dh, diámetro
hidráulico. f, coeficiente de fricción. n, coeficiente de rugosidad de Manning. C,
coeficiente de resistencia de Cházy. Los parámetros S, e, f, n de Manning y C de Chézy
se han obtenido (empíricamente) mediante la combinación del diagrama de Moody y la ley
universal de distribución de velocidad de Predtl-von Kárman, combinación que constituye
uno de los componentes del modelo IHRA.
En la Tabla 2 se indican las principales características hidráulicas de las secciones analizadas en el Llobregat y Cardener. Tanto la "C" de Chézy como la "n" de Manning se han obtenido mediante la ley logarítmica de distribución de velocidades aplicada a las dos velocidades que se toman a distintas profundidades en cada vertical de la sección transversal del cauce (Chow, 1990). Ambas adquieren valores semejantes a los recomendados en las tabulaciones según el tipo de cauce. En los tramos LL-56, LL-53, LL-60, LL-68, LL-102 y LL-91 que son canales naturales limpios, rectos y amplios con granulometría gruesa en la solera a base de guijarros, cantos rodados y algo de arena, se han obtenido valores de "n" que varían entre 0,027 y 0,038. Las tabulaciones recomiendan para este tipo de cauces , valores que oscilan entre 0,030 y 0,04. En los tramos LL-97 y C-39 cuyas soleras son de hormigón desgastado se ha obtenido un valor de n = 0,014, y las tabulaciones recomiendan para el hormigón no pulido una n = 0,014 ± 0,002. Los valores aparentemente inesperados de "n" son los que se dan en los tramos naturales C-42 y C-100, semejantes a los obtenidos para las soleras de hormigón. Ambos, C-42 y C-100, son canales sin vegetación acuática y con sustrato homogéneo de arenas finas y limpias.
La rugosidad relativa (e/Dh) con valores en torno o superiores a 0,2 en las estaciones LL-56, LL-53, LL-68, LL-102 y LL-91 nos permite prever que los caudales estimados por la fórmula de Manning van a diferir significativamente de los caudales aforados o circulantes por el río. Por el contrario, en los tramos LL-60, LL-97, C-42 y C-39, donde la rugosidad relativa (V/Dh) presenta valores aproximadamente contenidos en el intervalo 0,001 y 0,05, la ecuación de Manning predecirá caudales muy próximos a los circulantes. En este sentido, en la Tabla 3 se contrastan los caudales aforados con los estimados por las fórmulas de Manning y Chézy. Puede observarse que los menores errores se dan con la ecuación de Chézy, que no superan el 4% entre el caudal circulante y el estimado (en LL-102 con un 3,7%). Además estos errores adquieren valores positivos y negativos, es decir, en unos casos la fórmula de Chézy valora por exceso, en tanto que en otros por defecto.
| ESTACIÓN | CAUDAL AFORADO (L S-1) | Q-MANNING (L S-1) | Q-CHÉZY (L S-1) | ERROR (I) | ERROR (II)(%) | ERROR (III) (%) |
| LL-56 | 1.400 | 1752.78 | 1398.00 | -25.199 | .143 | 25.378 |
| LL-53 | 1.750 | 2182.11 | 1700.00 | -24.692 | 2.857 | 28.359 |
| LL-60 | 2.925 | 3086.96 | 2859.00 | -5.537 | 2.256 | 7.973 |
| LL-68 | 4.000 | 6477.31 | 4090.00 | -61.183 | -2.250 | 57.636 |
| LL-102 | 3000 | 370.02 | 311.00 | -23.342 | -3.667 | 18.979 |
| LL-97 | 15.060 | 15496.24 | 15192.00 | -2.897 | -.876 | 2.003 |
| LL-91 | 11.290 | 14036.81 | 11280.00 | -24.330 | .089 | 24.440 |
| C-42 | 2.200 | 2305.63 | 2205.00 | -4.801 | -.227 | 4.564 |
| C-39 | 3.065 | 3102.85 | 3020.00 | -1.235 | 1.468 | 2.743 |
| C-100 | 4.685 | 5215.53 | 44617.00 | -11.324 | 1.451 | 12.964 |
TABLA 3. Contraste de Caudales. Q-MANNING representa el caudal estimado con la
fórmula de Manning. Q-CHEZY es el caudal determinado con la ecuación de velocidad de
corriente de Chézy. ERROR (I), es la diferencia porcentual entre el caudal aforado y el
caudal determinado con la fórmula de Manning. ERROR (II) representa la diferencia
porcentual entre el caudal aforado y el caudal estimado con la ecuación de Chézy. ERROR
(III) es la diferencia en porcentaje entre los caudales de Manning y Chézy.
Por el contrario, los errores asociados a la fórmula de Manning en los casos en los que (e/Dh) Ê0,2, superan el 20%, alcanzándose un
valor del 61% en la estación LL-68, donde (e/Dh) = 0,56 (Tabla 2). La estación LL-68 de Balsareny es un tramo
ancho y de sección transversal muy irregular donde la fórmula de Manning predice un
caudal circulante de 6.447 l s-1, la de Chézy de 4.090 l s-1, y por
el cauce circulan unos 4.000 l s-1. En el tramo C-100 de Castellgalí se
aprecia un caso en el que (e/Dh) < 0,001, obteniéndose un error del 11,3%. Obsérvese
también en la Tabla 3 que el Error (I) o diferencia porcentual entre el caudal aforado y
el estimado por Manning es siempre negativo, lo que confirma la teoría de que cuando la
rugosidad relativa del canal (e/Dh) se encuentra fuera del citado intervalo de validez de la
fórmula de Manning, ésta sobrevalora los caudales circulantes (White, 1988).
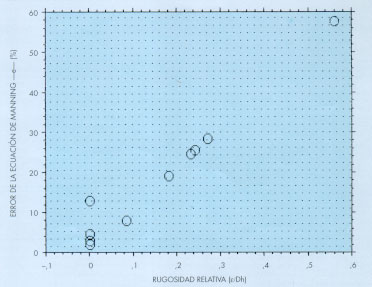
A efectos prácticos, cuando la rugosidad relativa 0,0002
> e /Dh >
0,1, los errores de la ecuación de Manning en la estima del caudal circulante superan el
10% (figura 2), pudiendo tener consecuencias importantes en el caso de la modelización
hidráulica de caudales ecológicos o de otros acontecimientos, donde dicha modelización
se utiliza para estimar características geométricas del cauce generadas por dichos
caudales, tal y como se demuestra en el siguiente apartado.
 |
|
3.2. MODELIZACIÓN HIDRÁULICA
DE CAUDALES ECOLÓGICOS
La modelización hidráulica se ensaya en dos tramos, El Collet d'Eina (LL-53) y La Coromina (G42). En LL-53, (e /Dh) = 0,27 (Tabla 3) y la aplicación de la ecuación de Manning es poco aconsejable. En C-42, (e/Dh) = 0,001, y tanto la ecuación de Manning como la de Chézy aportarían resultados equivalentes y precisos.
Para llevar a cabo la modelización hidráulica, hay que tener en cuenta que en las secciones transversales de los dos tramos, el radio hidráulico (Rh) se relaciona con el área de la sección mojada (A) y la profundidad de la lamina de agua o máximo calado (H) mediante sendas ecuaciones potenciales, cuyo ajuste estadístico se realiza con el método de los mínimos cuadrados ordinarios (figuras 3 y 4). Este ajuste potencial, implica que las secciones se aproximan a la forma trapezoidal. En la modelización hay que establecer la relación entre el caudal circulante (Q) y la profundidad del agua (H), partiendo del hecho de que aquél es el producto del área por la velocidad media: Q = V. A. De esta forma, se obtienen en cada tramo dos expresiones algebraicas para el caudal versus calado [Q = f(H)], una sustituyendo V por la ecuación de Manning, y la otra, sustituyéndola por la expresión de Chézy. Al mismo tiempo, de las figuras 3 y 4 se extrae la relación existente entre el radio hidráulico (Rh) y el calado (H) y entre el área mojada (A) y dicho calado, expresándose Q en función de este último (H). Por lo tanto, la modelización hidráulica en el caso que nos ocupa se resume en las siguientes expresiones:
Ecuación de Chezy
Q = C a S0.5 d b+0.5 H k (0,5+b) (8)
Ecuación de Marming
Q = (a/n) d b+2/3 S0,5 H k (b+2/3) (9)
Q=a db V Hbk (10)
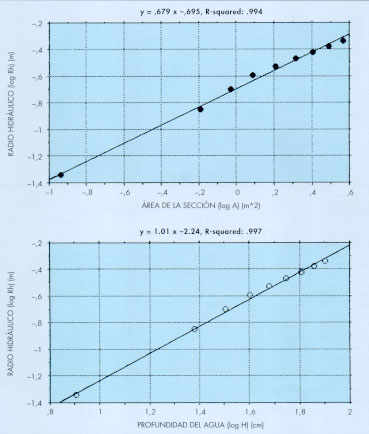 |
FIGURA 3. Relaciones existentes entre el radio hidráulico (Rh) con el área de la sección mojada (A) y la profundidad de la lámina de agua (H) en el tramo del río Llobregat LL-53 (El Collet d´Eina). Relaciones ajustadas a una fórmula potencial mediante mínimos cuadrados ordinarios. Se indica la ecuación rectificada con logaritmos decimales y el coeficiente de determinación de Pearson (r2). |
FIGURA 4. Relaciones existentes entre el radio hidráulico (Rh) con el área de la sección mojada (A) y la profundidad de la lámina de agua (H) en el trao del río Cardener C-42 (L a Coromina). Relaciones ajustadas a una fórmula potencial mediante mínimos cuadrados ordinarios. Se indica la ecuación rectificada con logaritmos decimales y el coeficiente de determinación de Pearson (r2). | 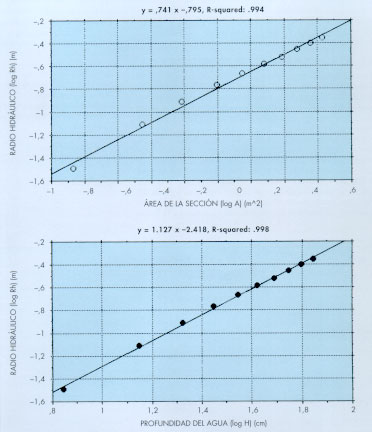 |
Siendo, Q el caudal circulante en m3 s-1. H, el calado o máxima
profundidad alcanzada por la lamina de agua en metros. V, la velocidad media de la
corriente en m s-1. , la pendiente de la línea de energía n el coeficiente de
rugosidad de Manning. C el coeficiente de resistencia de Chézy. "a" y
"b" son coeficientes empíricos que proceden de relacionar el área de la
sección mojada (A) con el radio hidráulico (Rh). "k" y "d", son
también coeficientes empíricos obtenidos a partir de la relación existente entre el
radio hidráulico (Rh) y la profundidad de la lamina de agua (H). a, b, k y d se obtienen
mediante mínimos cuadrados ordinarios regresionando las características morfométricas
de la sección húmeda con la ecuación potencial, tal y como se muestra en las citadas
figuras 3 y 4, y en la Tabla 4. Hay que señalar que no en todos los tramos la relación
Rh versus H y A versus H es la mas sencilla de tipo potencial, como la indicada en las
figuras 3 y 4. En otros casos dicha relación puede ser una recta (p.ej. C39), un
polinomio (LL-68), una ecuación potencial con asíntota horizontal, una expresión
logarítmica polinomial, etc. que dan lugar a ecuaciones muy distintas de (8), (9) y (10),
teniendo que resolverse de forma numérica o iterativa.
| COEFICIENTE MORFOMÉTRICO | EL COLLET D´EINA (LL-53) | LA COROMINA (C-42) |
| a | 10.423 | 11.668 |
| b | 1.462 | 1.341 |
| d | 0.604646 | 0.9878 |
| k | 1.0162 | 1.128 |
TABLA 4. Valores de los coeficientes morfométricos de la sección transversal
del cauce, utilizados para el ajuste de las ecuaciones de caudal circulante (8), (9) y
(10), correspondientes a los tramos de los ríos Llobregat (LL-53) y su afluente el
Cardener (C-42). a, b, d y k se obtienen mediante regresión lineal en las figuras (3) y
(4).
Las ecuaciones (8), (9) y (10) ajustadas a los tramos LL-53 y C-42 son las siguientes:
TRAMO DEL RÍO LLOBREGAT, LL-53: EL COLLET D'EINA
Ecuación de Chézy
Q = 2,786 H1.994 (11)
Ecuación de Manning
Q = 3,7437 H 2,113 (12)
Q=5VH 1,485 (13)
TRAMO DEL RÍO CARDENER, C-42: LA COROMINA
Ecuación de Chézy
Q = 4,612 H2,0766 (14)
Ecuación de Manning
Q = 5,185 H2,2646 (15)
Q = 7,0637 V H1,5126 (16)
El paso siguiente consiste en determinar los caudales ecológicos utilizando las ecuaciones de la (11) a la (16) de acuerdo con una serie de criterios biológicos que se indicaran más adelante. En otras ocasiones dichas ecuaciones son utilizadas para comprobar si los caudales ecológicos determinados de forma no hidráulica (p.ej. de forma hidrológica) como en los modelos RECE y de Medias Móviles de Palau (1994), se cumplen una serie de características de calado, velocidad de corriente, etc. En otros métodos, las relaciones no se establecen respecto al calado (H), sino con respecto al perímetro o anchura mojada no ponderada o ponderada (APU), como es el caso de los modelos de White (1976) e IFIM, citados en la introducción.
El carácter polémico de los caudales ecológicos radica en los criterios biológicos a tener en cuenta para determinarlos, que muchas veces dependen de la orientación de los gestores para los que se calculan dichos caudales (aunque no debiera ser así). Nosotros consideramos los siguientes cuatro criterios básicos, utilizados por el modelo RECE para calcular los caudales ecológicos:
1. Conservación del Paisaje Hidráulico. El objetivo es conseguir que en un tramo fluvial, que de forma natural es lótico o de aguas corrientes, el caudal ecológico mantenga ese aspecto de aguas corrientes o reofilo, y no produzca estancamientos de agua o pozas unidas entre sí por un escaso flujo. Y viceversa, aquellos tramos que de forma natural son remansos, el caudal ecológico debe seguir manteniendo la facies léntica o de aguas remansadas. Para la consecución de este objetivo se hace uso de la Vulnerabilidad Hidráulica (VH) definida por la fórmula (6). Un tramo es hidráulicamente sensible a la formación de estancamientos o pozas de agua, si VH > 0,2.
El coeficiente mórfico de Vedernikov (K) contenido en la fórmula de la VH tiene valores superiores a 0,5 en los dos tramos LL-53 y C-42, lo que nos permite afirmar que ambos tramos son hidraulicamente anchos, siendo algo más ancho C-42 que LL-53, y siendo algo más sensible a los estancamientos de agua LL-53 (VH = 0,316) que C-42 (VH = 0,254).
En los cauces hidráulicamente sensibles a la formación de pozas, donde VH > 0,2, el caudal ecológico nunca debe general un número de Reyno1ds (Re) inferior a 12.500, con el cual se asegura la turbulencia y continuidad del flujo. Utilizando la ecuación de Chézy, la velocidad media del flujo puede expresarse en función de Re mediante la siguiente fórmula, donde todos los términos son conocidos:
V = (Re v C2 S)1/3 (17)
La aplicación de esta fórmula a los tramos que nos ocupan nos permite establecer que:
1-a) En LL-53 para generar un Re = 12.500 se precisa una velocidad media del flujo no inferior a 20 cm s -1, a la que le corresponde un Rh = 8 cm y un calado máximo de 13,7 cm. Con la fórmula (11) o con la (13), se calcula que para evitar los estancamientos de agua (conservar el paisaje hidráulico) en LL-53, el caudal ecológico nunca podrá ser inferior a 53 ls-1.
2-b) En C-42, un Re = 12.500 da origen a una velocidad V = 20,5 cm s-1 con un Rh = 7 cm y un H = 13,20 cm. Las fórmulas (14) o (16) determinan que para evitar las pozas unidas por hilillos de agua, el caudal ecológico no debe ser inferior a 69 ls-1. Los dos casos extremos de la Tabla 2 son Balsareny (LL-68) y Castellgalli (C-100) donde para conservar el paisaje fluvial, la velocidad media de corriente no debe ser inferior a 16 cm s-1 y 32 cm s-1, respectivamente.
Mas adelante se muestra como los caudales ecológicos determinados para LL-53 y C-42 cumplen suficientemente este criterio de conservación del paisaje hidráulico.
2. Conservación de la Biodiversidad Fluvial. Ambos tramos, LL-53 y C-42, están habitados cuanto menos por invertebrados del bentos y peces, y el caudal ecológico debe general un perímetro mojado que por menos sea capaz de mantener 25 especies entre invertebrados y peces (Docampo, 1997). El menor de los caudales ecológicos que se indica en la Tabla 5 cumple este criterio.
| TRAMO | CHEZY PRIMAVERA |
MANNING PRIMAVERA |
CHEZY VERANO |
MANNING
VERANO |
CHEZY
QE-Ribera |
MANNING QE- Ribera |
| LL-53 | 1.006 | 1.240 | 357 | 397 | 4.787 | 6.735 |
| C-42 | 1.596 | 1.630 | 259 | 224 | 4.343 | 4.857 |
TABLA 5.
Caudales ecológicos en l s-1 generados por las ecuaciones de Chézy
y Manning en los tramos LL-53 (El Collet d´Eina) y La Coromina (C-42) durante
las épocas de primavera (abril, mayo y junio) y verano (julio, agosto y septiembre).
Estos caudales cumplen el criterio de conservar la biodiversidad fluvial representada
por invertebrados bénticos y peces, y generar un hábitat óptimo para los peces,
caracterizado por un flujo sin estrés hidráulico, cuyas condiciones son: VÍ
60 cm s-1 en primavera y verano, H Ê 60 cm para la primavera y HÊ25 cm para
el verano. QE-Ribera, representa el caudal ecológico que debe mantenerse durante
un período no superior a una semana, cuyo objetivo es irrigar las riberas, contribuyendo
con ello a su regeneración, conservación del bosque de galería (si lo hubiese)
y exportar nutrientes hacia el medio acuático, condición esta última de vital
importancia para el funcionamiento de los ecosistemas fluviales (Decamps &
Naiman, 1989). El caudal medio geométrico interanual en LL-53
3. Conservación de la Vegetación de Riberas. En el período de mayor caudal medio circulante por aportaciones naturales, que en el caso que nos ocupa es Mayo en C-42 y Junio en LL-53, durante una semana debe mantenerse un caudal ecológico que alcance los rizomas o el sistema radicular de la vegetación de riberas, con ello se contribuye a la exportación de nutrientes desde las riberas hasta el medio acuático y a la conservación del bosque de galería (Tabla 5).
4. Protección de la Fauna Piscícola. Tomando como base las curvas de calidad del hábitat con respecto al calado (H) y a la velocidad media de corriente (V) para una comunidad amplia de especies ícticas, representadas en la figura 5, se establece que:
4-a) En verano o en el periodo de estiaje con bajos caudales, el caudal ecológico debe general un calado mínimo de 25 cm, es decir, H Ê 25 cm. En primavera, el caudal ecológico debe generar una H Ê 60 cm.
4-b) Tanto en primavera como en verano, el caudal ecológico no debe dar lugar a una velocidad de corriente superior a los 60 cm s-1, V Í 60 cm s-1, a partir de la cual el índice de calidad del hábitat de los peces desciende por debajo del 50% (figura 5).
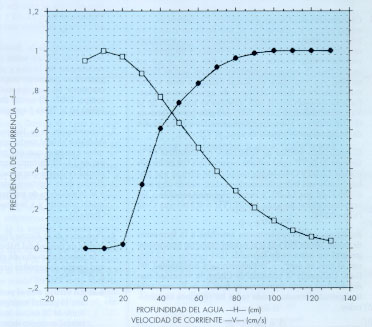 |
FIGURA 5. Frecuencia de ocurrencia de las comunidades de peces con respecto a la velocidad media de la corriente (curva de cuadrados vacíos) y con respecto a la profundidad máxima de la lámina de agua (curva de círculos negros). El ICH o el Índice de Calidad del Hábtat es la frecuencia de ocurrencia de las especies con respecto a V y H. Estas curvas {f(H) y f(V)} se han obtenido de forma estadística (aplicando la familia de transformaciones de Box-Cox, 1962, a los hstogramas de frecuencias) a partir de una matriz de más de 2000 datos de medidas de velocidad y profundidades de lámina de agua de tramos fluviales habitados por teucha (Salmo trutta m. fario), barbo de Graells (Barbus graellsií), piscardo (Phoxinus phoxinus), loina (Chondrostoma toxostoma) y locha de roca (Noemacheilus barbatulus). A partir del punto de intersección de ambas curvas se define un criterio general para la determinación de caudales ecológicos: HÊ 60 y VÍ 60 cm s-1 |
La estación LL-53 se encuentra en Muy Buen Estado Ecológico (de acuerdo con
la terminología de la citada Propuesta de Directiva Marco de Protección de Aguas
de la Unión Europea), caracterizado por aguas limpias ultraoligosaprobias, y
donde no es preciso utilizar el criterio de calidad del agua en la estima de
caudales ecológicos. La estación C-42 se encuentra moderadamente eutrofizada
y si que habría que tener en cuenta la posible variación de las cargas de nitrógeno
y fósforo en la determinación de dichos caudales, utilizando balances de masas
como los del QUAL2E u otros, algo que resulta ser extenso para este trabajo.
Tomando H = 25 cm en las ecuaciones (11) y (12) para LL-53 y (14) y (15) para C-42, se comparan los caudales ecológicos que generan en verano las fórmulas de Chézy y Manning. Igualmente, tomando H = 60 cm, se comparan dichos caudales en primavera. Las fórmulas (13) y (16) donde interviene V, sirven para corroborar que la velocidad de flujo generada por los caudales ecológicos estimados no sobrepase el criterio de los 60 cm s-1. Por otro lado, en LL-53 para conservar la vegetación de riberas H = 131,2 cm y en C-42 H = 97,155 cm, valores éstos que se sustituyen en las fórmulas de Chézy y Manning para cumplir con el citerior 3.- de conservación de la vegetación de riberas.
En la Tabla 5 se expresan los caudales ecológicos así calculados. En la estación C-42 se puede observar que tanto Manning como Chézy predicen en primavera, verano y para la ribera, caudales ecológicos muy similares, ya que la rugosidad relativa del canal se encuentra dentro del intervalo de validez de la fórmula de Manning (0,0002 > e /Dh > 0,1). Por el contrario, en LL-53 donde e /Dh > 0,1, Manning y Chézy solamente predicen caudales ecológicos similares en verano, es decir, para niveles bajos de caudal. En primavera, los caudales difieren en un 23%, y en el caudal de conservación de las riberas (QE-Ribera), la diferencia llega a ser de hasta el 40,7%. Se han obtenido diferencias mucho más acusadas, incluso para el verano, en los ensayos realizados para la estación LL-68 donde e /Dh = 0,561.
Como conclusión se establece que, todos los modelos de determinación de caudales ecológicos (simulación de White, IFIM o el PHABSIM, Método Vasco, RECE, algunos balances de masas, etc.), siempre utilizan para la simulación hidráulica la ecuación de velocidad de corriente de Manning de régimen uniforme, corno si de un axioma se tratase. Tal proceder no es correcto en todos los casos y más aún en ríos o canales abiertos naturales donde la rugosidad relativa del canal (e/Dh) es muy variable y tiene una influencia muy importante en la validez de dicha fórmula. A efectos prácticos, la ecuación de Manning es un buen estimador de la velocidad media del flujo cuando 0,0002 > e/Dh > 0,1. Fuera de este intervalo sus errores son significativos y transmisibles a la determinación de caudales ecológicos o de las características hidráulicas de los cauces generadas por éstos. La ecuación de Chézy ajustada a través del coeficiente de fricción del canal (diagrama de Moody) es valida para cualquier valor de la rugosidad relativa (e/Dh) y tan exacta como la de Manning en el citado intervalo de rugosidades intermedias (ver Tabla 3). En consecuencia, la modelización hidráulica de caudales ecológicos debe basarse en la ecuación de Chézy ajustada de la forma descrita en el modelo IHRA, con el fin de no cometer errores en aquellos casos en los que ecuación de Manning es inviable o poco precisa.
| BINNS, N. A. 1982. Habitat quality index procedures
mannual. Wyorning Game and Fish Department Cheyenne. 209 pp BOVEE, K. D. 1982. A guide to stream habitat analysis using the Instream Flow Incremental Methodology . Instr. Flow Inf. Paper 12. USDI Fish and Wildl. Serv. Whashington. 248 pp. BOX, G. E. P. & TIDWELL, P. W 1962. Transformations of the independent variables. Technometrics, 4: 531-550. BOX, G. E. P. & JENKINS, G. M. 1976. Time series analysis: forecasting and control. Holden Day. BROWN, L. C. & BARNWELL, JR. 1987. Modelo mejorado de calidad de agua en ríos: QUAL2E y QUAL2E-UNCAS. Documentación y Manual del Usuario. EPA/600/3-87/007. Environmental Research Laboratory. U.S. Environmental Protection Agency. CHOW, V. T. 1990. Hidráulica de los canales abiertos. Diana. Mexico. 631 pp. COLEBROOK, C. F. 1939. Turbulent flow in pipes, with particular reference to the transition between the smooth and rough pipe laws--- J. Inst, Civ. Eng., 11 : 133 - 156. DECAMPS, H. & NAIMAN, R. J. 1989. La ecología de los ríos. Mundo Científico, 91 (9): 470-479. DELOS, C. G.; RICHARDSON, W L.; DEPINTO, J. V; ROGERS, D. W; RYGWELSKI, K.; WETHINGTON, R.; AMBIOSE, R. B. & JOHN, J. P. ST. 1983. Technical guidance manual for performing waste load al locations. Book 11: Stream and Rivers, Capter 3: Toxic Substances. EPA. DOCAMPO, L. 1996. Ajuste de la integral de la ecuación normal y su aplicabilidad en hidrología y calidad de aguas. Ingeniería Civil, 103 : 83 - 90. DOCAMPO, L. 1997. Determinación de caudales ecológicos mediante el método vasco y el modelo R.E.C.E. (Régimen Estacional de Caudales Ecológicos). Obra Científica inscrita en el Registro General de la propiedad Intelectual del Estado Español (N' Registro: 131-4234), divulgada como conferencia en el curso "Aspectos Ambientales de la Gestión del Agua" de la EOI (Escuela de Organización Industrial) celebrado en Zaragoza en Octubre de 1997. Madrid. 43 pp. DOCAMPO, L. 1988a. Modelo I.H.R.A.: Ingeniería Hidraulica de Ríos y Acequias. Programa informático registrado como Obra Científica en el Registro General de la propiedad Intelectual del Estado Español. Nº Registro: 4.803. Madrid. 26pp. DOCAMPO, L. 1998b. Conjunto de ecuaciones fisicoquímicas del agua (C.E.FA.)(I). Programa informático registrado como Obra Científica en el Registro General de la propiedad Intelectual del Estado Español. N2 Registro: 4.744. Madrid. 22pp. DOCAMPO, L. & G. DE BIKUÑA, B. 1995. The Basque Method for determining instream flows in Northern Spain. Rivers, 4 (4): 292 - 311. GARCíA DE JALÓN, D. 1990. Técnicas hidrobiológicas para la fijación de caudales ecológicos mínimos. En: Libro homenaje al profesor D.M. Garcia de Viedma, 183-196. A. Ramos, A. Notario & R.R. Baragaño (eds.) FUCOVASA, UPM. Madrid. GLOVER, R. E. & FLOREY, Q. L. 1951. Stable channel profiles. U.S. Bureau of Reclamation, Hydraulic Laboratory Report, No. Hyd-325. Septiembre. 276 pp. Junta D'Aigües. 1996. Determinación de caudales ecológicos de los ríos Llobregat y Cardener. Generalitat de Catalunya. Informe Técnico no publicado. Barcelona. 64 pp. KING, H. W. 1954. Handbook of hydraulics. McGraw-Hill. New York. KOLUPAILA, S. 1956. Methods of determination of the kinetic energy factor. The Port Engineer. Calcuta, 5 (1): 12-18. MACARTHUR, R. H. & WILSON, E. 0. 1967. The theory of island biogeography. New Jersey. Princeton University Press. MOODY, L. F. 1944. Friction factors for pipe flow. ASME Trans., 66: 671 - 684. PALAU, A. 1994. Los mal llamados caudales "ecológicos". Bases para una propuesta de cálculo. Obra Pública, N' 28 (Ríos 11): 84-95. PEÑA, D. 1989. Estadística, modelos y métodos. 2. Modelos lineales y series temporales. Alianza Universidad. Madrid. 745 pp. SPIEGEL, M. R. 1993. Estadística. McGraw-Hill. Madrid. 556pp. UN. 1954. Standards for methods and records of hydrologic measurements. United Nations Economic Commission for Asia and the Far East, Flood Control Series, No. 6, pp: 26 30. Bangkok. WHITE, F. M. 1988. Mecánica de fluidos. McGRawHill. Mexico. 757 pp. WHITE, R. G. 1976. A methodology for recommending stream resource maintenance flows for large rivers. Proces, on Instream Flow Needs Symp.: 376 -386. |
(*) HURIEM (Sociedad de Investigación y
Gestión de Humedales, Ríos y Embalses). Ortuella (Vizcaya)